Kezdőlap


Feladat:	F.2595	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1986/december, 440 - 441. oldal		PDF \| MathML
Témakör(ök):	Beírt gömb, Köréírt alakzatok, Egyenes körkúpok, Térfogat, Számtani-mértani egyenlőtlenségek, Alakzatok súlypontja (tömegközéppontja), Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 1986/szeptember: F.2595

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a kúp alapkörének sugarát $r$ -rel, magasságát $m$ -mel, a kúp félnyílásszögét pedig $α$ -val. Legyen még a gömb sugara 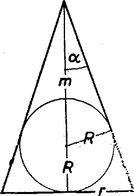$R$ .

Az ábra alapján felírhatjuk a következő összefüggéseket:

\begin{matrix} r = m \cdot tgα, \\ R = (m - R) sin α, \end{matrix}

és ebből

\begin{matrix} R = \frac{m \cdot sin α}{1 + sin α} . \end{matrix}

Írjuk fel a gömb

V_{g}

, illetve a kúp

V_{k}

térfogatát:

\begin{matrix} V_{g} = \frac{4 π}{3} \cdot {(\frac{m \cdot sin α}{1 + sin α})}^{3}; V_{k} = \frac{{(m \cdot tgα)}^{2} \cdot π \cdot m}{3} . \end{matrix}

Feladatunk azt kérdezi, hogy mekkora lehet a

\frac{V_{g}}{V_{k}}

hányados. A fentiek szerint

\begin{matrix} \frac{V_{g}}{V_{k}} = \frac{\frac{4 π}{3} \cdot {(\frac{m \cdot sin α}{1 + sin α})}^{3}}{\frac{{(m \cdot tgα)}^{2} \cdot π \cdot m}{3}} = \frac{4 \cdot sin α (1 - sin α)}{{(1 + sin α)}^{2}} . \end{matrix}

Írjuk ezt a következőképpen:

\begin{matrix} 2 \cdot \frac{2 sin α}{1 + sin α} \cdot \frac{1 - sin α}{1 + sin α} \end{matrix}

(1)

és vegyük észre, hogy

\begin{matrix} \frac{2 \cdot sin α}{1 + sin α} + \frac{1 - sin α}{1 + sin α} = 1. \end{matrix}

(2)

Mivel

α

hegyesszög, (1) második és harmadik tényezője pozitív, (2) szerint pedig e két tényező összege állandó. A jól ismert

a \cdot b \leq {(\frac{a + b}{2})}^{2}

egyenlőtlenség alapján

\begin{matrix} \frac{2 \cdot sin α}{1 + sin α} \cdot \frac{1 - sin α}{1 + sin α} \leq {(\frac{1}{2})}^{2}, \end{matrix}

és itt pontosan akkor van egyenlőség ‐ tehát (1) akkor maximális ‐, ha

\begin{matrix} \frac{2 \cdot sin α}{1 + sin α} = \frac{1 - sin α}{1 + sin α} . \end{matrix}

Ebből

sin α = \frac{1}{3}

, és ilyenkor

\frac{V_{g}}{V_{k}} = \frac{1}{2}

.
Egy gömb a köréírt forgáskúpnak tehát legfeljebb a felét tölti ki.

Megjegyzés. A talált esetben a gömb középpontja egybeesik a kúp súlypontjával.