Kezdőlap


Feladat:	F.2590	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1986/december, 438 - 440. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Háromszögek nevezetes tételei, Euler-egyenes, Súlypont, Magasságpont, Körülírt kör középpontja, Számtani sorozat, Feladat
Hivatkozás(ok):	Feladatok: 1986/szeptember: F.2590

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyenek a háromszög szögei $α, β, γ .$ A feladat szövegéből következik, hogy egyik szög sem derékszög, mert tangenseik léteznek. A szögek betűzéséről feltehető, hogy $tgα\leqtg β \leqtg γ .$ Ekkor csakis ebben a sorrendben alkothatnak számtani sorozatot, tehát

\begin{matrix} tgα+ tgγ=2 tgβ. \end{matrix}

(1)

Írjuk be mindkét oldalon a tangens definícióját és szorozzunk

cos α \cdot cos β \cdot cos γ

-val. Kapjuk, hogy

\begin{matrix} cos β (sin α \cdot cos γ + cos α \cdot sin γ) = 2 \cdot sin β \cdot cos α \cdot cos γ . \end{matrix}

A bal oldalon a zárójelben az addíciós tétel szerint éppen

sin (α + γ)

áll, s ez

sin (π - α - γ) = sin β

-val egyenlő.

0 < β < π

miatt

sin β \neq 0

, egyszerűsíthetünk vele, s így azt kapjuk, hogy

\begin{matrix} cos β = 2 cos α \cdot cos γ . \end{matrix}

(2)

Most belátjuk, hogy (2) ekvivalens azzal, hogy

sin 2 α

sin 2 β

sin 2 γ

(ilyen sorrendben) számtani sorozatot alkot, tehát

\begin{matrix} sin 2 α + sin 2 γ = 2 \cdot sin 2 β . \end{matrix}

(3)

A (3) bal oldalát szorzattá alakítjuk, majd felhasználjuk, hogy

sin (α + γ) = sin β

, a jobb oldalon pedig a kétszeres szög szinuszára vonatkozó összefüggést használjuk. Így kapjuk, hogy

\begin{matrix} 2 \cdot sin β \cdot cos (α - γ) = 4 \cdot sin β \cdot cos β . \end{matrix}

Egyszerűsítünk

2 \cdot sin β

-val (ami nem

0

), majd mindkét oldalból levonunk

cos β

-t:

\begin{matrix} cos (α - γ) - cos β = cos β . \end{matrix}

Tudjuk, hogy

- cos β = cos (α + γ)

. Ha ezt beírjuk a bal oldalra, és alkalmazzuk az addíciós tételt, ekkor azt kapjuk, hogy

\begin{matrix} 2 \cdot cos α \cdot cos γ = cos β, \end{matrix}

ami nem más, mint (2).
Lépéseink megfordíthatók, így (2) valóban pontosan akkor igaz, ha

sin 2 α,

sin 2 β

sin 2 γ

(ebben a sorrendben) számtani sorozat, és éppen ezt akartuk bizonyítani.

II. megoldás. Tegyük fel, hogy az

A B C

háromszög szögeire teljesül (1). Ekkor a háromszög nem lehet derékszögű, hiszen mindhárom szögének van tangense. Megmutatjuk, hogy ekkor a háromszög tompaszögű sem lehet. Ha ugyanis

β

tompaszög, akkor a másik két szög hegyes, és így

tgβ< 0

tgα> 0

és

tgγ> 0,

márpedig ekkor (1) nem állhat fönn. Ha viszont például

α

tompaszög, akkor (1) bal oldalát

tgα+tg γ =-tg(β + γ)+tg γ

alakba írva

γ

β + γ

egyaránt

0

és

π / 2

közé esik, tehát

tg (β+γ) >tg γ,

s így a bal oldal negatív, míg

tgβ> 0,

hiszen

α

és

β

nem lehet egyszerre tompaszög.

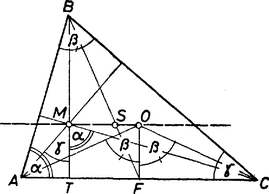
Ha tehát (1) igaz, akkor az

A B C

háromszög hegyesszögű. Legyen

O

a köré írt körének középpontja,

M

a magasságpontja,

T

B

-ből induló magasságának talppontja és

F

A C

oldal felezőpontja (ábra). Ekkor

M

is,

O

is a háromszög belsejében van és

A M T ∢ = B C A ∢ = γ

C M T ∢ = B A C ∢ = α

(mert merőleges szárú szögek), tehát

\begin{matrix} tgα+ tgγ=\frac{C T}{T M}+\frac{T A}{T M}=\frac{C A}{T M}. \end{matrix}

Másrészt a kerületi és középponti szögek tétele miatt

A O C ∢ = 2 β

, így a fele,

A O F ∢ = β

, tehát

\begin{matrix} tg β = \frac{A F}{F O} = \frac{A C}{2 F O} . \end{matrix}

(1) tehát a

\frac{C A}{T M} = \frac{A C}{F O}

azaz

T M = F O

alakba írható. Minthogy

O

és

M

A C

-nek ugyanazon a partján van, és

M T

párhuzamos

O F

-fel (mindkettő merőleges

A C

-re), ezért azt kaptuk, hogy (1) pontosan akkor igaz, ha a hegyesszögű

A B C

háromszögben

O M

, a háromszög Euler egyenese párhuzamos

A C

-vel.
Az Euler-egyenesen az

S

súlypont is rajta van, s ennek távolsága

A C

-től

\frac{1}{3} B T = \frac{m_{b}}{3}

, ezért az Euler egyenes pontosan akkor párhuzamos

A C

-vel, ha

O F = \frac{m_{b}}{3}

is fennáll. Az Euler egyenes párhuzamossága tehát egyenértékű azzal, hogy az

A O C

háromszög területe harmada az

A B C

háromszög területének:

\begin{matrix} 3 t_{A O C} = t_{A B C} . \end{matrix}

(4)

Másrészt hegyesszögű háromszögben

t_{A B C} = t_{A O C} + t_{C O B} + t_{B O A}

, ahonnan (4) szerint azt kapjuk, hogy

\begin{matrix} 2 t_{A O C} = t_{C O B} + t_{B O A} . \end{matrix}

(5)

Miután pedig

t_{A O C} = \frac{1}{2} r^{2} sin 2 β

t_{C O B} = \frac{1}{2} r^{2} sin 2 α

és

t_{B O A} = \frac{1}{2} r^{2} sin 2 γ

, az (5) egyenletet

\frac{r^{2}}{2}

-vel végigosztva, éppen a kívánt

\begin{matrix} 2 sin 2 β - sin 2 α + sin 2 γ \end{matrix}

egyenlőséget kapjuk.

Megjegyzés. Könnyű belátni, hogy a bizonyítás lépései megfordíthatók, tehát hegyesszögű háromszögben az alábbi négy állítás ekvivalens:
1.

tgα+tg γ =2 \cdottg β .

2. Az Euler-egyenes párhuzamos az

A C

oldallal.
3.

t_{A O B} + t_{B O C} = 2 t_{A O C} .

sin 2 α + sin 2 γ = sin 2 β .

Nem nehéz megmutatni, hogy tompaszögű háromszögben e négy állítás egyike sem lehet igaz.