Feladat: F.2589 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Beke T. ,  Benczúr A. ,  Bereczky Á. ,  Bóna M. ,  Cynolter G. ,  Grallert Ágnes ,  Horváth 335 A. ,  Pál Gábor ,  Rimányi R. ,  Szalay Gy. ,  Tasnádi T. 
Füzet: 1987/április, 150 - 152. oldal  PDF  |  MathML 
Témakör(ök): Egyenlő szárú háromszögek geometriája, Magasságvonal, Sokszög lefedések, Feladat
Hivatkozás(ok):Feladatok: 1986/május: F.2589

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel a lefedés egyenlő hosszúságú szakaszokkal is megoldható, nyomban ezt bizonyítjuk.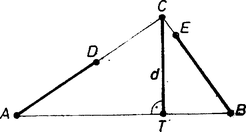
A lefedni kívánt ABC háromszög leghosszabb oldala (vagy ezek egyike) legyen AB. Az AB oldalhoz tartozó magasság T talppontja AB belső pontja. A lefedő szakaszok hosszát (d) e magasságéval megegyezőnek választjuk. A szakaszrendszer valamennyi elemének egyik végpontja az AB oldalra illeszkedik, másik végpontja pedig az AC vagy a BC oldalon van.

 
 
1. ábra
 

Mivel a csúcspontok hovatartozása az oldalakat illetően nem egyértelmű, a háromszög csúcsait lefedő szakaszokat külön adjuk meg. Az A csúcsot fedje az AC oldalon fekvő AD szakasz, a B csúcsot a BC oldalon fekvő BE szakasz, a C csúcsot pedig a CT magasságszakasz. ( D és E az AC, ill. BC oldalnak az A, ill. B csúcstól d távolságra levő pontja. D és E létezik, mivel AC>d és BC>d.) (1. ábra).
A lefedéshez diszjunkt szakaszok rendszerét kell megadnunk, ezért a lefedő szakaszok végpontjai kölcsönösen meghatározzák egymást. Így p1. ha a C csúcsot a CT szakasszal fedjük le, a T pont lefedésére ugyancsak a CT szakaszt írjuk elő.
A szakaszrendszer elemeinek AB-re illeszkedő, A-tól, B-től és T-től különböző végpontját a továbbiakban Pt, a másik végpontját Rt jelöli. Rt aszerint legyen az AC vagy a BC oldalon, hogy Pt az AT vagy a BT szakasz belső pontja.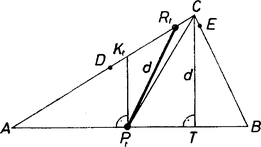
 
 
2. ábra
 

E megszorítás mellett is előfordul, hogy valamely Pt-hez két megfelelő Rt pont található. Ezért kikötjük még, hogy az RtPtT∢ legyen hegyesszög. Így már bármely Pt-hez egy és csak egy Rt tartozik. Messe ugyanis az AB oldalra Pt-ben állított merőleges az AC vagy BC oldalt Kt-ben. Mivel KtPt<d<CPt, a KtC szakasz egy és csak egy Rt pontot tartalmaz, amelyre RtPt=d (2. ábra). Az RtPtT∢ nyilván hegyesszög. Itt jegyezzük meg, hogy valamennyi Rt pont a DC vagy az EC szakasz belső pontja. Ha p1. Pt az AT szakasz belső pontja, az APtRt háromszög Pt -nél fekvő belső szöge tompaszög. Ezért ARt>PtRt=d=AD. Rt nem eshet a C csúcsba sem, mivel PtC>d.
Különböző Pt pontokhoz nem tartozhat ugyanaz az Rt pont, ellenkező esetben létrejönne olyan egyenlő szárú háromszög, amelynek alapon fekvő szögei közül az egyik hegyesszög, a másik tompaszög volna. Így Pt és Rt kölcsönösen meghatározzák egymást.
A szakaszrendszer megadásánál tekintettel voltunk arra, hogy a háromszög határvonalának pontjaira egy és csak egy lefedő szakasz illeszkedjék; ahol szükséges volt, ezt be is bizonyítottuk. Már csak azt kell bizonyítanunk, hogy a háromszöglemez bármely belső pontján is egy és csak egy halad át szakaszaink közül.
Legyen először a vizsgált pont a CT magasság belső pontja. Ezen a CT magasság áthalad, más lefedő szakasz viszont nem, mivel a CT magasságon kívül minden lefedő szakasz benne van a CT egyenes által meghatározott félsíkok egyikében.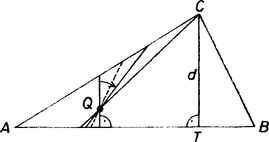
 
 
3. ábra
 

Tekintsük most az ATC háromszög valamely Q belső pontját (3. ábra). Állítsunk a Q ponton át merőlegest az AB oldalra. Ennek az ATC háromszögbe eső szakasza d-nél kisebb. A merőleges egyenest forgassuk a Q pont körül olyan irányba, hogy az AC egyenessel alkotott metszéspontja a C csúcshoz közeledjék. Az egyenesnek az ATC háromszögbe eső szakasza folytonosan és szigorúan monoton növekszik. (Ez egyszerűen belátható annak alapján, hogy tompaszögű háromszögben a tompaszöggel szemközti oldal a legnagyobb.) A  QC egyenesnek a háromszögbe eső darabja már nagyobb d-nél. Ezért a mondott forgatás során az egyenes ACT háromszögbe eső szakasza egy és csak egy helyzetben lesz d hosszúságú. Ez a szakasz az általunk megadott szakaszrendszer eleme.
A BTC háromszög belső pontjaira ugyanígy végezhetjük a bizonyítást.
A feladat megoldását ezzel befejeztük.
 

Megjegyzés. A megoldásban lényegében azt használtuk fel, hogy egy derékszögű háromszög ‐ az ATC , illetve a BTC ‐ lefedhető a megadott módon a befogójával ‐ a TC-vel ‐ egyenlő hosszúságú szakaszokkal. Az alábbiakban egy korábbi feladat eredményét felhasználva igazoljuk ezt az állítást.
A 2316. gyakorlat megoldásában (lásd az 1986. novemberi számban, a 385‐386. oldalon) megmutattuk, hogy egy 2r sugarú K kör kerületén, annak belsejében csúszás nélkül gördülő r sugarú k kör kerületének tetszőleges pontja a K egy átmérőjén mozog.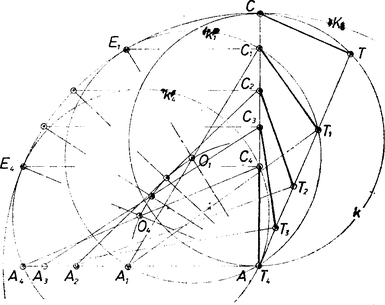
 
 
4. ábra
 

Tekintsük az ATC háromszöget a körülírt körével együtt ‐ legyen ez a k kör ‐ és foglaljuk ezt a kétakkora sugarú K körbe a 4. ábrán látható módon. Ekkor tehát az A pont a K középpontjába esik, a két kör pedig a C pontban érinti egymást.
Rögzítsük ebben a helyzetben az ATC háromszöget, a k kört pedig a CT húrjával együtt gördítsük a K kerületén addig a helyzetig, amíg a T pont ‐ amely az idézett állítás szerint az AT átmérőn mozog ‐ a kör középpontjába, A-ba jut.
Mivel a C pont eközben a CA átmérőn mozog, a k-val együtt mozgó CT húr éppen az előírt módon "söpri végig'' az ATC háromszöget.