Kezdőlap


Feladat:	F.2568	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1986/november, 369 - 371. oldal		PDF \| MathML
Témakör(ök):	Rekurzív eljárások, Mértani sorozat, Fibonacci-sorozat, Számsorozatok, Teljes indukció módszere, Feladat
Hivatkozás(ok):	Feladatok: 1986/február: F.2568

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy létezik olyan mértani sorozat, amelyre teljesül (1). Keressük tehát $a_{n}$ -et $a_{1} \cdot q^{n - 1}$ alakban, ahol $a_{1} > 0$ és $q > 0$ . Az (1) összefüggés szerint kapjuk, hogy ha $n \geq 1$ , akkor

\begin{matrix} a_{1} \cdot q^{n + 1} = a_{1} \cdot q^{n - 1} - a_{1} \cdot q^{n}, & (2) \\ ahonnan q^{2} = 1 - q . \end{matrix}

Ennek az egyenletnek a pozitív megoldása

\frac{\sqrt[]{5} - 1}{2}

. Ha most

a_{1} > 0

tetszőleges, akkor az

a_{n} = a_{1} {(\frac{\sqrt[]{5} - 1}{2})}^{n - 1}

sorozat minden tagja pozitív, és mivel lépéseink megfordíthatók, a sorozatra teljesül (2) és (1) is.

II. megoldás. Az alábbiakban azt is belátjuk, hogy a feladatnak nincs más megoldása, vagyis ha egy pozitív tagú

a_{n}

sorozatra teljesül (1), akkor az

a_{n}

szükségképpen mértani sorozat. Vizsgáljuk ehhez az

a_{n}

sorozat szomszédos elemeinek hányadosait, azaz legyen

b_{n} = \frac{a_{n + 1}}{a_{n}}

. Ekkor

b_{n} > 0

és (1) szerint

\begin{matrix} b_{n + 1} = \frac{1}{b_{n}} - 1 minden n \geq 1 egészre . \end{matrix}

(3)

Mivel

b_{n + 1}

is pozitív, (3)-ból kapjuk, hogy

b_{n} < 1

, azaz minden

n \geq 1

-re

\begin{matrix} 0 < b_{n} < 1. \end{matrix}

(4)

b_{n + 1}

-re is igaz, vagyis

0 < \frac{1}{b_{n}} - 1 < 1

, ahonnan

\begin{matrix} \frac{1}{2} < b_{n} < 1, \end{matrix}

és innen újra

b_{n + 1}

(3)-beli alakját beírva

\frac{1}{2} < \frac{1}{b_{n}} - 1 < 1

, ahonnan

\begin{matrix} \frac{1}{2} < b_{n} < \frac{2}{3} minden n - r e . \end{matrix}

(5)

Látható, hogy a

b_{n}

értékeire kapott újabb korlátok

(\frac{1}{2} és \frac{2}{3})

jobbak a korábbiaknál (0 és 1). A gondolatmenetet megismételve további javulás várható ‐ nézzük meg ezért ezt a lépést általában.
Legyen tehát

0 \leq u_{k} < b_{n} < v_{k} \leq 1

minden

n

-re, azaz

u_{k}

és

v_{k}

k

-adik lépésben kapott korlátok

(u_{1} = 0, v_{1} = 1)

. A (4)-től (5)-ig vezető lépéseket elvégezve most azt kapjuk, hogy minden

n

-re

\begin{matrix} u_{k + 1} = \frac{1 + u_{k}}{2 + u_{k}} < b_{n} < \frac{1 + v_{k}}{2 + v_{k}} = v_{k + 1} . \end{matrix}

k

-ra vonatkozó teljes indukcióval könnyen igazolható, hogy a

(k + 1)

-edik lépésben kapott újabb korlátok,

u_{k + 1}

és

v_{k + 1}

valóban jobbak az előzőknél, azaz

u_{k} < u_{k + 1}

és

v_{k + 1} < v_{k}

.
Ha ugyanis

f (x) = \frac{1 + x}{2 + x}

és

x_{0}

jelöli az

f (x) = x

egyenlet pozitív megoldását ‐

x_{0} = \frac{\sqrt[]{5} - 1}{2}

‐ akkor az indukciós bizonyításokban arra van szükség, hogy ha

0 < x < x_{0}

, akkor

x < f (x) < x_{0}

, illetve ha

x_{0} < x

, akkor

f (x) < x

, hiszen

u_{k + 1} = f (u_{k})

és

v_{k + 1} = f (v_{k})

. Az utóbbi állítások pedig leolvashatók az

f (x)

és az

x

függvények grafikonjáról (lásd az ábrát).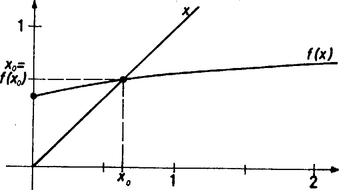

Másfelől

\begin{matrix} 0 < v_{k + 1} - u_{k + 1} = \frac{v_{k} - u_{k}}{(2 + v_{k}) (2 + u_{k})} < \frac{1}{4} (v_{k} - u_{k}), \end{matrix}

ahonnan

\begin{matrix} 0 < v_{k} - u_{k} < \frac{1}{4^{k - 1}}, hiszen v_{1} - u_{1} = 1. \end{matrix}

Ez azt jelenti, hogy az

[u_{k}, v_{k}]

egymásba skatulyázott zárt intervallumok hossza 0-hoz tart, így ha minden

n

-re

b_{n} \in [u_{k}, v_{k}]

minden

k

-ra, akkor

b_{n}

állandó, az

a_{n}

tehát mértani sorozat. Hányadosát

q

-val jelölve

q = b_{n} = {lim}_{k \to \infty}^{} u_{k} = {lim}_{k \to \infty}^{} v_{k}

.
Mivel

u_{k}

konvergens, ezért

u_{k + 1}

is az és

\begin{matrix} q = {lim}_{k \to \infty}^{} u_{k + 1} = {lim}_{}^{}_{k \to \infty}^{} \frac{1 + u_{k}}{2 + u_{k}} = \frac{1 + {lim}_{}^{}_{k \to \infty}^{} u_{k}}{2 + {lim}_{}^{}_{k \to \infty}^{} u_{k}} = \frac{1 + q}{2 + q}, \end{matrix}

ahonnan

q

-ra az első megoldásban kapott

q^{2} + q - 1 = 0

egyenlet adódik. Ennek pozitív gyökével mint hányadossal és tetszőleges pozitív kezdőértékkel elkészített mértani sorozatok adják a feladat összes megoldását.

Megjegyzések. 1. Ha felírjuk az

u_{k}

és

v_{k}

sorozatok néhány elemét, akkor az alábbi törteket kapjuk:

\begin{matrix} \frac{0}{1}, \frac{1}{2}, \frac{3}{5}, \frac{8}{13}, \frac{21}{34}, ..., illetve \\ \frac{1}{1}, \frac{2}{3}, \frac{5}{8}, \frac{13}{21}, \frac{34}{55}, ... \end{matrix}

Látható, hogy a

↓ ↗ ↓ ↗ ↓ ↗ ↓ ↗

séma szerint haladva mindkét esetben a Fibonacci-féle sorozatot kapjuk, amelynek elemeire fennáll az

f_{n + 2} = f_{n + 1} + f_{n}

összefüggés. Ha

f_{0} = 0

, akkor

\begin{matrix} u_{k} = \frac{f_{2 (k - 1)}}{f_{2 k - 1}}, v_{k} = \frac{f_{2 k - 1}}{f_{2 k}}, k = 1, 2, ... \end{matrix}

A második megoldás állítása most már adódik abból az ismert tényből, hogy a Fibonacci-sorozat szomszédos elemeinek hányadosa,

f_{n} / f_{n + 1}

\frac{\sqrt[]{5} - 1}{2}

értékhez tart; a páros

n

-ekhez tartozó részsorozat monoton növekedően, páratlan

n

-ekre pedig monoton fogyóan.
2. Az (1) összefüggés szerint az

a_{n}

sorozat minden egyes eleme a megelőző kettő segítségével számítható ki: a sorozatot egy úgynevezett rekurzió adja meg. Ha nem írnánk elő, hogy a sorozat elemei pozitív számok, akkor az első két elemet,

a_{1}

-et és

a_{2}

-t tetszés szerint megválasztva a további elemek (1) alapján számolhatók. A második megoldásból kiderül, hogy ha

a_{1} : a_{2} \neq (\sqrt[]{5} - 1) / 2

, akkor az így elkészített sorozatnak nem lehet minden eleme pozitív.
A sorozatok ilyen módon történő megadása igen gyakori: a számtani sorozatot például az

a_{n + 1} = a_{n} + d

, a mértani sorozatot az

a_{n + 1} = a_{n} \cdot q

, a fentiekben is előkerült Fibonacci-sorozatot pedig az

a_{n + 2} = a_{n + 1} + a_{n}

összefüggés adja meg. Az ilyen módon megadott sorozatok bizonyos tulajdonságai a rekurzív összefüggésből is leolvashatók, ám gyakran szükség van az

n

-edik elemet közvetlenül megadó explicit összefüggésre. A számtani sorozat esetén ilyen az

a_{n} = a_{1} + (n - 1) \cdot d

, a mértani sorozatra az

a_{n} = a_{1} \cdot q^{n - 1}

, az általános Fibonacci-sorozatra pedig az első pillanatra meghökkentő

\begin{matrix} a_{n} = A \cdot {(\frac{1 + \sqrt[]{5}}{2})}^{n - 1} + B \cdot {(\frac{1 - \sqrt[]{5}}{2})}^{n - 1} . \end{matrix}

Ilyen explicit formula felírására nincsen általános módszer, azonban a rekurziók egy jól jellemezhető osztályára ismeretes a probléma megoldása. A feladatban szereplő

a_{n + 2} = a_{n} - a_{n + 1}

rekurzió pedig ebbe az osztályba tartozik.
Az ilyen rekurziók általános alakja:

a_{n + 2} = c_{1} \cdot a_{n + 1} + c_{2} \cdot a_{n}

, ahol

c_{1}

és

c_{2}

adott konstansok. Esetünkben

c_{1} = - 1

c_{2} = 1

. (Ha

c_{1} = c_{2} = 1

, akkor éppen a Fibonacci-sorozathoz jutunk.)
Az általános megoldás a

q^{2} = c_{1} \cdot q + c_{2}

egyenlet ‐ a rekurzió úgynevezett karakterisztikus egyenlete ‐ gyökeinek, a

q_{1}

-nek és a

q_{2}

-nek a segítségével írható fel (

q_{1}

és

q_{2}

komplex számok is lehetnek):

\begin{matrix} ha q_{1} \neq q_{2}, akkor a_{n} = A \cdot q_{1}^{n - 1} + B \cdot q_{2}^{n - 1}; \\ ha q_{1} = q_{2}, akkor a_{n} = A \cdot q_{1}^{n - 1} + B \cdot n \cdot q_{1}^{n - 1} \end{matrix}

alakú az általános megoldás.
Az

A

és a

B

itt tetszőlegesen választott konstansok; amennyiben a rekurzív összefüggés mellett a sorozat első két elemét is megadjuk és ezzel egyértelműen meghatározzuk a sorozatot, akkor

A

és

B

a sorozat első két elemére is érvényes formulákból adódó kétismeretlenes egyenletrendszer megoldásai.
A fenti állítás bizonyítása ‐ és némi általánosítása ‐ megtalálható például N. I. Vilenkin: Kombinatorika című könyvének (Műszaki Könyvkiadó, 1971) 168‐174. oldalán.
Esetünkben a karakterisztikus egyenlet,

q^{2} = 1 - q

gyökei

\begin{matrix} q_{1} = \frac{\sqrt[]{5} - 1}{2}, q_{2} = \frac{- \sqrt[]{5} - 1}{2} . \end{matrix}

Az általános eredmény szerint tehát az (1) rekurzió összes megoldása

\begin{matrix} A \cdot q_{1}^{n - 1} + B \cdot q_{2}^{n - 1} alakú . \end{matrix}

Mivel

| q_{1} | < 1

, ezért az összeg első tagja,

A \cdot q_{1}^{n - 1}

a 0-hoz tart; másfelől

q_{2} < - 1

miatt

B \neq 0

esetben a második tag nem korlátos sem alulról, sem pedig felülről. Ez azt jelenti, hogy ha

B \neq 0

, akkor a sorozatnak nem lehet minden eleme pozitív.