Kezdőlap


Feladat:	F.2564	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Drasny G. , Figeczky G. , Keleti T. , Rimányi R.
Füzet:	1986/október, 300 - 302. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Háromszögek hasonlósága, Másodfokú (és arra visszavezethető) egyenletek, Trigonometriai azonosságok, Egyenlő szárú háromszögek geometriája, Rombuszok, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1986/január: F.2564

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a kör középpontja $O$ , a harmadoló pontok a köríven $C$ és $D$ , az $O C$ , $O D$ egyenes és az $A B$ egyenes metszéspontja pedig rendre $E, F$ .
Az $A B C D$ és az $E F C D$ négyszög szimmetrikus az $A B$ húr felező merőlegesére, ezért $E F$ és $C D$ párhuzamosak (mindkét szakasz merőleges a szimmetriatengelyre), ezenkívül $E A = B F = A B$ , mert a feladat feltétele szerint $E A + B F + A B = 3 A B$ . A $D O C$ és $F O E$ háromszögek így nyilván hasonlóak; a következőkben meghatározzuk ennek a hasonlóságnak az arányát.

1. ábra

A körbe írt

A O D, D O C, C O B

egyenlő szárú háromszögekben a szárszögek egyenlőek, mert

D

és

C

harmadolópontok, így a három háromszög egybevágó. Emiatt

A D = D C = C B

és

A D O ∢ = O D C ∢ = O F A ∢

. A

D A F

háromszög tehát egyenlő szárú:

A F = A D

. Az

A F C D

négyszög tehát rombusz, továbbá a

D O C

és

F O E

háromszögek hasonlóságának aránya innen

\begin{matrix} D C : F E = A F : F E = 2 A B : 3 A B = 2 : 3. \end{matrix}

Ennek alapján már megszerkeszthető egy megfelelő

A, B

pontpár. Az

O

középpontú,

r

sugarú

k

körön tetszőlegesen kijelöljük a

D

pontot. Az

F

pont a

D O

egyenes és az

O

középpontú

\frac{3}{2} r

sugarú kör

O

-n túli metszéspontja. Az

A

és

C

pontokat a

D F

felező merőlegesének és a

k

körnek a metszéspontjaiként kapjuk, hiszen egy négyszög pontosan akkor rombusz, ha átlói merőlegesen felezik egymást. Mivel

D F

átmérő, ezért valóban rombuszt kapunk. Végül a

B

pont a

k

kör és az

A F

egyenes metszéspontja.
A fenti okoskodás megfordításával belátható, hogy a kapott

A, B

pontpár kielégíti a feladat feltételeit.

II. megoldás. 1. Jelöljük a keresett

A B

ívhez tartozó kisebbik középponti szöget

A O B ∢ = 6 x

-szel ‐ ahol tehát

0^{\circ} < 6 x < 180^{\circ}

‐, ebből számítás alapján adunk jellemzést

A

-ra,

B

-re. Az I. megoldás jelöléseit használjuk, legyen még

A B

felezőpontja

M

. Igy

O M

az ábra szimmetriatengelye,

M

E F

szakaszt is felezi,

F

B

-nek

3

-szoros nagyítása az

M

centrumból.
A nagyobbik

A O B

szög mértékszáma

360^{\circ} - 6 x

, ennek harmada

A O D ∢ = 120^{\circ} - 2 x, így M O D ∢ = 3 x + (120^{\circ} - 2 x) = 120^{\circ} + x,

és ennek kiegészítő szöge

M O F ∢ = 60^{\circ} - x

, hegyesszög. Az

E F = 3 A B

követelményből

M F = 3 M B

, azaz

tg (60^{\circ} - x) = 3 tg (3 x)

, és ismert azonosságok alapján

\begin{matrix} \frac{\sqrt[]{3} - tg x}{1 + \sqrt[]{3} tg x} = \frac{3 tg x (3 - {tg}^{2} x)}{1 - 3 {tg}^{2} x}, \end{matrix}

majd szorzattá alakításokkal,

tg x = u

jelöléssel

\begin{matrix} \frac{\sqrt[]{3} - u}{1 + \sqrt[]{3} u} = \frac{3 u (\sqrt[]{3} + u)}{1 - \sqrt[]{3} u} \cdot \frac{\sqrt[]{3} - u}{1 + \sqrt[]{3} u} . \end{matrix}

A föltevés szerint

0^{\circ} < x < 30^{\circ}

0 < u < 1 / \sqrt[]{3}

, így a bal oldali kifejezés, ami egyben a jobb oldal második tényezője is, pozitív szám. Ezért a jobb oldal első tényezője

1

-gyel egyenlő. Ebből

u

-ra a következő egyenlet adódik:

\begin{matrix} 3 u^{2} + 4 \sqrt[]{3} u - 1 = 0, \end{matrix}

ennek egyetlen pozitív gyöke pedig

\begin{matrix} u = tg x = \frac{\sqrt[]{5} - 2}{\sqrt[]{3}} . & (1) \end{matrix}

2. Bár ezzel már meghatároztuk az

A O B ∢ = 6 x

szöget, mégis ‐ a kérdés egyszerűségére tekintettel ‐ szívesen látnánk az

A

B

pontoknak körzővel és vonalzóval való megszerkesztését is. Ez (1) alapján lehetséges ugyan, de meglehetősen hosszadalmas, helyette rövidebb úton először az

O M F

háromszöghöz hasonlót szerkesztünk.
Föntebbi számításunk szerint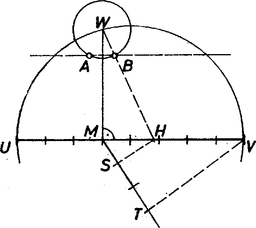

\begin{matrix} tg M F O ∢ = tg (30^{\circ} + x) = \\ = \frac{\frac{1}{\sqrt[]{3}} + \frac{\sqrt[]{5} - 2}{\sqrt[]{3}}}{1 - \frac{\sqrt[]{5} - 2}{3}} = ... = \sqrt[]{\frac{3}{5}} . \end{matrix}

2. ábra

Legyen egy egyenesen

U M = 3

egység, és folytatva

M V = 5

egység, messe az

U V

átmérőjű kört az

M

-ben

U V

-re emelt merőleges

W

-ben, ekkor tüstént

\begin{matrix} tg M V W ∢ = \\ = \frac{M W}{M V} = \frac{\sqrt[]{3 \cdot 5}}{5} = tg M F O ∢, \end{matrix}

tehát az

M V W

háromszög hasonló az 1. ábra

M F O

háromszögéhez. Most már az

M

-en átmenő, az

U V

-től különböző félegyenesre fölmérve az

M S = 1

M T = 3

szakaszokat, az

S

-en átmenő és

T V

-vel párhuzamos egyenessel kimetsszük az

M V

szakasz

H

harmadoló pontját.

W

körül megrajzoljuk az adott körrel egyenlő sugarú kört, ebből

W H

kimetszi

B

-t, és ezen át

U V

-vel párhuzamost húzva kapjuk

A

-t.

B. T.

Megjegyzések. 1. Az (1)-nél egyszerűbb szerkesztések olvashatók ki a következőkből is:

\begin{matrix} tg 3 x = \sqrt[]{\frac{5}{27}}, sin 3 x = \sqrt[]{\frac{5}{32}}, cos 3 x = \sqrt[]{\frac{27}{32}}, \end{matrix}

5 + 27

átmérőjű félkört kellene használnunk.
2. A két megoldás eredményeit azonosíthatjuk azáltal, hogy kiszámítjuk az I. megoldásból

tg M F O ∢ = A N / N F

értékét, ahol

N

A C

szakasz felezőpontja.