Kezdőlap


Feladat:	F.2551	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1986/április, 156 - 157. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Szögfelező egyenes, Beírt kör, Beírt kör középpontja, Paralelogrammák, Feladat
Hivatkozás(ok):	Feladatok: 1985/november: F.2551

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a $B C$ oldal felezőpontját $F$ -fel, a beírt körnek az $A C$ , $B C$ befogón levő érintési pontját $B_{1}$ -gyel, ill. $A_{1}$ -gyel. Felhasználjuk, hogy minden háromszögben a szokásos jelölések mellett $C B_{1} = C A_{1} = s - c$ , esetünkben pedig, mivel az $O A_{1} C B_{1}$ idom négyzet, azért a beírt kör sugara: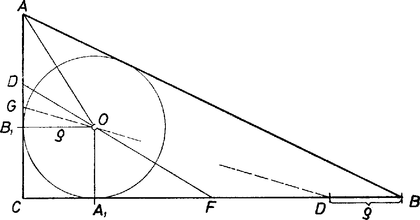

\begin{matrix} ϱ = s - c = \frac{a + b - c}{2} . \end{matrix}

1. ábra

Megmutatjuk, hogy a kérdéses

D

pont a

B_{1}

tükörképe az

A C

befogó

G

felezőpontjára nézve, vagyis

D A = B_{1} C = ϱ

. A

D O B_{1}

és

O F A_{1}

háromszögek nyilvánvaló hasonlóságából

\begin{matrix} D B_{1} : B_{1} O = O A_{1} : A_{1} F, \end{matrix}

ahonnan

\begin{matrix} D B_{1} = \frac{ϱ^{2}}{A_{1} F} = \frac{ϱ^{2}}{\frac{a}{2} - ϱ} = \frac{{(a + b - c)}^{2}}{2 (a - 2 ϱ)} . \end{matrix}

A számlálót ‐ kifejtve és a Pitagorasz-tétel alkalmazásával ‐ szorzattá alakítjuk:

\begin{matrix} 2 c^{2} - 2 a c - 2 b c + 2 a b = 2 (c - a) (c - b), \end{matrix}

a nevező pedig a második

ϱ

-képlet átrendezésével

2 (c - b)

-vel egyenlő. Így ‐ ismét

ϱ

alapján ‐

\begin{matrix} D B_{1} = \frac{(c - a) (c - b)}{c - b} = c - a = b - 2 ϱ, \end{matrix}

ennélfogva

D C = b - ϱ

és

A D = A C - D C = ϱ

, amint állítottuk.
Ezek alapján a vizsgálandó arány az

A O B_{1}

derékszögű háromszög alapján

\begin{matrix} \frac{A D}{D C} = \frac{B_{1} O}{A B_{1}} = tg B_{1} A O ∢ = tg \frac{α}{2}, \end{matrix}

hiszen

A O

felezi a

C A B

szöget.

Megjegyzések. 1. Szigorúan véve

A_{1} F = | \frac{a}{2} - ϱ |

kifejezés lett volna a helyes, de mindjárt átgondoltuk, hogy a

2 ϱ > a

nagyságviszony lehetetlen.
2. Könnyű belátni, hogy

D

az a pont, ahol az

A B C

háromszög

A C

oldalához "hozzáírt külső érintő kör'' érinti ezt az oldalt.
Ez a számolás útján nyert "szerkezeti összefüggés'' újabb megoldás keresésére sarkallhat.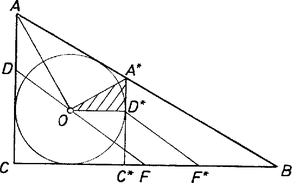

II. megoldás. Rajzoljuk meg a beírt kör

A C

befogóval párhuzamos másik érintőjét. Messe ez a háromszög oldalait az

A^{*}

, ill.

C^{*}

pontban, az érintési pontot pedig jelölje

D^{*}

(2. ábra).

2. ábra

A megoldás alapötlete az ‐ a 2. megjegyzés értelmében most már nyílt kártyákkal játszunk ‐, hogy a

B C^{*} A^{*}

háromszöget

B

-ből a

B C A

háromszögbe nagyítva

D^{*}

D

-be megy át. Ezt persze most újra bizonyítanunk kell, de a lépések "maguktól adódnak''.
Szükség van a

C^{*} B

szakasz felezőpontjára ‐ legyen ez

F^{*}

. Ekkor

F F^{*} = B F - B F^{*} = \frac{1}{2} (B C - B C^{*}) = \frac{1}{2} C C^{*}

, és ez épp

ϱ

, hisz

C C^{*}

A B C

háromszög beírt körének átmérőjével egyenlő.
Az

O D^{*} F^{*} F

négyszögben tehát

O D^{*} = F F^{*} = ϱ

, és ez a két oldal nyilván párhuzamos is. A négyszög tehát paralelogramma, így másik két oldala is párhuzamos, és nekünk éppen erre volt szükségünk, hiszen az említett nagyítás során

F^{*} D^{*}

F

-en átmenő,

F^{*} D^{*}

-gal párhuzamos egyenesbe, tehát az

F D

-be megy át. Mivel pedig

A^{*} C^{*}

A C

be megy át, a

D^{*}

képe valóban a

D

.
Most akár betorkollhatnánk az előző megoldás gondolatmenetébe is, azonban az eddigiek alapján gyors befejezést találhatunk.
A talált hasonlóság miatt a keresett

\frac{A D}{D C}

arány

\frac{A^{*} D^{*}}{D^{*} C^{*}}

-gal egyenlő.

D^{*} C^{*} = ϱ = D^{*} O

, így a keresett arány az

A^{*} D^{*} O

derékszögű háromszögben

tg A^{*} O D^{*} ∢

.
Mivel

A^{*} O A ∢ = 90^{\circ}

‐ az

A

és az

A^{*}

csúcsú, párhuzamos szárú szögek szögfelezőiről van szó ‐ másrészt

O D^{*} ⊥ A C

A^{*} O D^{*}

és az

O A C

szögek merőleges szárú hegyesszögek, és így egyenlők.
A keresett arány ezért az

O A C

szögnek ‐ tehát az

A

-nál levő szög felének ‐ a tangense.