Kezdőlap


Feladat:	F.2547	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1986/május, 198 - 199. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Háromszögek hasonlósága, Egyenlő szárú háromszögek geometriája, Szögfelező egyenes, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1985/október: F.2547

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C$ háromszög $B A C$ szögének nagyságát $α$ -val és válasszuk úgy a betűzést, hogy $C B A ∢ = 2 α,$ $A B C ∢ = 4 α$ , (tehát $α = 180^{\circ} : 7$ ) legyen. Legyenek továbbá a szögfelezőknek a szemben fekvő oldalon levő metszéspontjai rendre $A_{1}, B_{1}, C_{1}$ . Azt látjuk be, hogy az ezek által meghatározott háromszögben 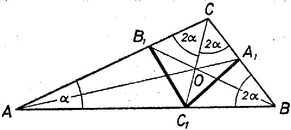$C_{1} A_{1} = C_{1} B_{1}$ .

Ez a

C_{1} A_{1} B

és

C_{1} B_{1} C

háromszögek egybevágóságából következik, ha beláttuk hozzá, hogy

C_{1} B = C_{1} C

A_{1} B = B_{1} C

, ugyanis a köztük levő

C_{1} B A_{1}

és

C_{1} C B_{1}

szögek mértékszáma a föltevés, ill. a felezés folytán

2 α

C_{1} B = C_{1} C

, mert a

C_{1} B C

háromszögben a velük szemben levő szögek egyenlők.
A második egyenlőséghez három háromszögpár hasonlóságára hivatkozunk, azok alapján 2 ‐ 2 szakasz arányának egyenlőségét írjuk fel, végül az ezek összeszorzásával adódó egyenlőséget egyszerűsítjük.

O

-val a három szögfelező közös pontját jelöljük. A hasonlóságok alapja mindhárom esetben 2 ‐ 2 szög egyenlősége, esetleg közös volta. Az

A B A_{1}

és az

A C O

; az

A B C

és a

B C O

, valamint a

B B_{1} C

és a

B C O

háromszögek hasonlósága alapján

\begin{matrix} \frac{A_{1} B}{A B} = \frac{O C}{A C}, \frac{A B}{B C} = \frac{A C}{B O}, \frac{B C}{B_{1} C} = \frac{B C}{C O} . \end{matrix}

Valóban, innen

\begin{matrix} \frac{A_{1} B}{B_{1} C} = 1. \end{matrix}

Ezt akartuk belátni, és így az állítást bebizonyítottuk.