Feladat: F.2545 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bíró József 
Füzet: 1986/március, 110 - 113. oldal  PDF  |  MathML 
Témakör(ök): Egyenlő szárú háromszögek geometriája, Középvonal, Koordináta-geometria, Paralelogrammák, Négyszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 1985/október: F.2545

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. E-vel és F-fel az AC, ill. BD átló felezőpontját jelöljük, ezenfölül a BC oldal felezőpontját G-vel, az AB és a CD oldalak közös hosszát pedig 2k-val (1. áb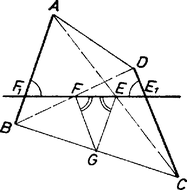ra).

 
 
1. ábra
 

Ekkor
EG=AB2=k=DC2=FG,
mert itt az első és az utolsó hosszúság középvonal az ABC, ill. DCB háromszögben. Így EFG egyenlő szárú háromszög. Ez valódi háromszög, mert E és F egymástól a feladat föltevése alapján, G-től pedig a négyszög konvexsége miatt különböző. (Az A és D csúcsok a BC egyenesnek ugyanazon a partján vannak, nincsenek rajta BC-n, ennélfogva ugyanezek érvényesek a felezéssel nyert E és F pontokra is.)
Eszerint a GE és GF egyenesek egyenlő szögeket zárnak be a vizsgálandó EF egyenessel. Mivel pedig GE egyirányú BA-val és GF a CD-vel, ezért BA és CD is egyenlő szöget alkotnak EF-fel. Ezt kellett bizonyítanunk.
 

 Bíró József (Bonyhád, Petőfi S. Gimn., III. o. t.)
 

Megjegyzések. 1. Akinek a tudatában ott él, hogy két metsző egyenes között nagyságra nézve általában kétféle szög van (egyetlen kivétel a merőlegesség, ami éppen ezért különleges eset), az kissé bizonytalannak érzi az állítást. Valami ilyen ködlik: az EF és AB egyenespár, valamint az EF és CD pár szögei közül lehet egyenlőket összeválogatni. Pontosítani lehet az állítást úgy, ha megadjuk a menetirányt az EF egyenesen pl. E-től F felé. Ekkor a négyszög belsejében levő szögek az egyenes bal oldalán egyenlők, tehát a jobb oldalán is. (Most már rájövünk, hogy máshogy nem is lehet, különben AB és CD párhuzamosak lennének, ami azt jelentené, hogy ABCD paralelogramma, vagyis E és F egybeesnek.)
2. A megoldás gondolatmenetével úgy is bizonyítható az állítás, ha G helyett az AD oldal H felezőpontját használjuk fel. Szóra sem volna érdemes ez a meglátás, ha nem lehetne valami érdekeset kiolvasni belőle, elvégre egyelőre csak arról van szó, hogy a kiszemelt AB és CD oldalak egyenrangúak, tehát a további két oldal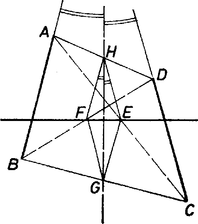, BC és DA is.
 
 
2. ábra
 

Nos, ha G-t és H-t egyszerre használjuk fel, akkor az EGFH négyszögnek mind a négy oldala k, emiatt átlói, EF és GH merőlegesek (2. ábra). Akkor pedig a merőleges szárú (hegyes-)szögek tétele alapján a GH egyenes is egyenlő szögeket zár be az AB és CD oldalak egyeneseivel. Ami érvényes a csúcsok A és C, valamint B és D párba állítására, az igaz a másik, A és D, valamint B és C párba állításra is. (Egy tréfás kifejezés módosításával: mégiscsak volt haszna, hogy két ágyúval lőttünk egyetlen verébre.)
3. Miért szerepel a szövegben a ,,konvex'' szó? Mert az iskolában alig jut idő nem konvex idomok ,,igényes'' vizsgálatára. (A konvex idom földbirtokra emlékeztet; még a konkáv is, de hurkolt négyszög már nem.) A megszokás hatására a legtöbb beküldő akkor is csak konvex négyszöggel foglalkozna, ha ez a megszorítás nem szerepelne a szövegben.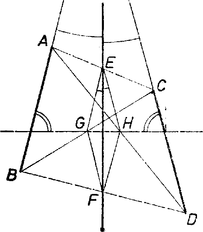
 
 
3. ábra
 

Nézzük meg hát, mi lesz, ha 1‐2. ábráinkon C és D betűzését fölcseréljük, tehát ABCD(A) hurkolt négyszög (3. ábra). (A kiinduló 4 pont kölcsönös helyzete ugyanaz.) Most lesz jó, hogy már előbb nem egyedül G-t vettük segítségül, hanem H-t is: a rombusz csúcsai ugyanazok, csupán E és F az előbbi H és G helyén adódnak ‐ és viszont. Tehát az állítás hurkolt négyszögre is érvényes. (Vázoljon fel az olvasó nem hurkolt, konkáv esetet is!)
4. Lehetne bizonyítani az állítást vektorokkal is, kihasználva, hogy EF→ nem 0-vektor. Kiderül, hogy a bizonyítás nem használta ki a négyszög konvex voltát. (A vektor-módszer még megfogalmazni is nehézkesen tudná ezt a tényt.)
Inkább arra lenne jó ez a bizonyítás, hogy az éppen frissen megismert vektorokkal megbarátkoztasson.
5. Így ,,felvértezve'' fogadja az olvasó a következő koordináta-geometriai megoldást is! E mellé tudatosan nem adunk ábrát. Az ábrák tulajdonképpen csak a tanulás időszakára valók ‐ hacsak nem konkrét helyzetet vizsgáló feladatról van szó.
II. megoldás. A föltevés folytán az AB és CD egyenesek nem párhuzamosak, hiszen különben az A,B,C,D pontnégyes konvex burka paralelogramma volna: AB párhuzamos CD-vel, és így vagy az lenne, hogy E,F azonosak, vagy (hurkolt esetben) az EF egyenes párhuzamos lenne AB-vel, CD-vel.
Jelöljük pontjaink koordinátáit a megválasztandó koordináta-rendszerben már előre így:
A(a1,a2),B(b1,b2),C(c1,c2),D(d1,d2),E(e1,e2),F(f1,f2),
 tehát
ei=ai+ci2ésfi=bi+di2,i=1,2.
Válasszuk a derékszögű rendszer x-tengelyét úgy, hogy az AB, CD oldalak ezen levő vetületei egyenlők legyenek:
|b1-a1|=|d1-c1|.(1)
Ez azt jelenti, hogy az AB, CD egyeneseknek az x-tengellyel bezárt hegyes szöge egyenlő (az előbbiek szerint ugyanis az x-tengely nem lehet párhuzamos egyikükkel sem). A távolságnak koordinátákkal való (x2-x1)2+(y2-y1)2 kifejezése, az AB=CD föltevés, valamint (1) alapján az y-tengelyre való vetületek is egyenlők:
|b2-a2|=|d2-c2|,(2)
tehát AB-nek és CD-nek az y-tengellyel bezárt hegyes szögei is egyenlők.
Ha mármost (1)-ben az abszolútérték-jelekben álló különbségek előjele ellentétes:
b1-a1=c1-d1,vagyisb1+d1=a1+c1,
tehát f1=e1, akkor azt kaptuk, hogy az EF egyenes merőleges az x-tengelyre, párhuzamos az y-tengellyel, ennélfogva az állítás igaz.
Ha pedig (1) felbontása így alakul:
b1-a1=d1-c1,(1a)
akkor (2) felbontása csak a következő lehet:
b2-a2=-(d2-c2),(2a)
ugyanis a megegyező előjelű megválasztás (1a)-val együtt azt jelentené, hogy AB párhuzamos CD-vel, amit kizártunk. Mármost (2a)-ból
b2+d2=a2+c2,azazf2=e2,
tehát EF az x-tengellyel párhuzamos, az állítás változatlanul igaz. A bizonyítást befejeztük.