Kezdőlap


Feladat:	F.2541	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Beke T. , Blahota I. , Bodor Cs. , Bóna M. , Borbás T. , Bortel L. , Csombor Cs. , Csott R. , Cynolter G. , Deák Csaba , Drahos Enikő , Erdélyi Z. , Fabó Gy. , Hajnal Z. , Horváth 572 L. , Ittzés G. , Kántor A. , Kelemen Eszter , Kintli L. , Király Andrea , Kiss 999 Z. , Klug R. , Majzik I. , Miró J. , Mohos Z. , Montágh B. , Pecsenye B. , Pinczés Sz. , Rimányi R. , Sass B. , Szalay Gy. , Vargay P. , Várkonyi V. , Veres Ildikó , Zaránd G. , Zsigmond L.
Füzet:	1986/március, 106 - 109. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Tengely körüli forgatás, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Kocka, Térfogat, Trapézok, Feladat
Hivatkozás(ok):	Feladatok: 1985/szeptember: F.2541

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A leírt ,,átlós'' metszetek egyértelműen meghatározzák az illető kockákat. Például mivel $A A_{1} = a$ , azért $A C = a \sqrt[]{2}$ , és a téglalapot $A C$ felező merőlegese körül derékszöggel elfordítva, megkapjuk a $B D D_{1} B_{1}$ metszetet. A metszetek közös $O$ középpontja egyben a kockák közös centruma. A feladatban szereplő közös $S$ sík mindkét kockának szimmetriasíkja. A feltételben említett forgatás térbeli $t$ tengelye pedig ‐ az $O$ -n átmenő $, S$ -re merőleges egyenes ‐ a feladatban szereplő átlós metszetek olyan forgási szimmetriatengelye, amely körül $180^{\circ}$ -kal elfordítva önmagukba jutnak. Ezért $t$ átmegy a $B B_{1}$ és $D D_{1}$ , ill. $F F_{1}$ és $H H_{1}$ élek felezőpontjain, amelyeknek $O$ -tól mért távolsága egyformán $A C / 2 = a / \sqrt[]{2}$ , tehát a két élpár $1 - 1$ tagja metszi egymást, metszéspontjuk $K$ , ill. $K_{1}$ (1. ábra). A két kocka a $t$ körüli $90^{\circ}$ -os elfordítással is átmegy egymásba.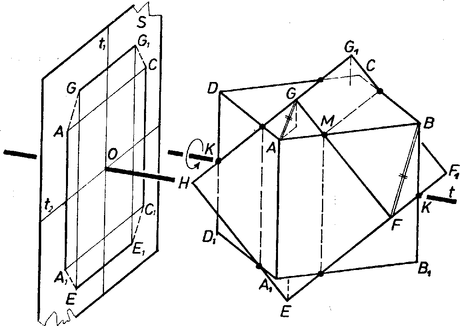

1. ábra

A vizsgálandó test örökli a két kockától, hogy az

S

-re való tükrözés, valamint a

t

körüli

90^{\circ}

-os elfordítások önmagába viszik át. Van még

2

további közös szimmetriasíkjuk is. Ezek a szimmetriák megkönnyítik a térfogatszámítást.
További metsző élpárok is vannak az alakzaton. Egy ilyen az 1. ábra betűzése mellett

A B

és

G F

‐ és további

7

szimmetrikus társ-élpár. Ugyanis az

A

G

B

F

csúcsok egy síkban vannak, mert az

A G

és

F B

egyenesek párhuzamosak. Jelöljük az

A C

és

E G

lapbeli átlók

S

-beli felező merőlegesét

t_{1}

-gyel, ill.

t_{2}

-vel, akkor

A G

párhuzamos e két újabb tengely egyik szögfelezőjével, és ugyanez érvényes

F B

-re is, mert

B F B_{1} F_{1}

négyzet, és

B B_{1} | | t_{1}

F F_{1} | | t_{2}

.
Eszerint az

A G B F

négyszög trapéz és átlói egyenlők,

A B = F G = a

. Ezek metszéspontját

M

-mel jelöljük, és mindjárt kiszámítjuk

M A = M G

és

M B = M F

részeik hosszát. Az

A G

szakasz átfogó egy olyan egyenlő szárú derékszögű háromszögben, amelyben a befogók hossza

(E G - A A_{1}) / 2 = a (\sqrt[]{2} - 1) / 2

, így

A G = a (1 - \frac{1}{\sqrt[]{2}})

. Hasonlóan

B F = \frac{a}{\sqrt[]{2}}

. Ezek szerint

\begin{matrix} A M : M B = A M : (a - A M) = A G : B F = (1 - \frac{1}{\sqrt[]{2}}) : (\frac{1}{\sqrt[]{2}}), \end{matrix}

amiből

\begin{matrix} A M = a (1 - \frac{1}{\sqrt[]{2}}), B M = \frac{a}{\sqrt[]{2}} . \end{matrix}

2. A térfogatszámításhoz az első kockából indulunk ki, és a másodikat odaképzelve leírjuk azokat a részeket és kiszámítjuk térfogatukat, amelyek az első kockából a másodikon kívülre esnek. Könnyű olyan nézeteket rajzolni az alakzatról, amelyekben a második kocka egy-egy lapját ,,élben'' látjuk (a lap vetülete egyenes szakasz).

2. ábra

A 2. ábrán a nézőirány az

A A_{1}

él, egyben a

G E

átló iránya, így a második kocka

E F G H

és

E_{1} F_{1} G_{1} H_{1}

lapjait egyenes szakaszoknak látjuk, és ezek az

A M N

és

C Q P

egybevágó, egyenlő szárú derékszögű háromszögeket metszik le az első kocka nézetéből, amely csupán az

A B C D

négyzet. Itt

N

és

Q

M

tükörképei az

A C

, ill.

B D

tengelyre nézve,

P

pedig e kettőnek közös képe ugyanezen tengelyekre.
Valójában egybevágó hasábokat metszenek le a síkok, az

E F G H

lap által lemetszettnek az alapja az

A M N

háromszög, oldaléle (magassága)

A A_{1} = a

, így e két hasáb együttes térfogata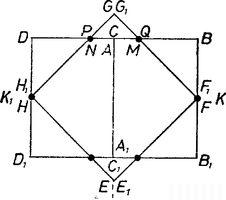

\begin{matrix} 2 \cdot \frac{1}{2} \cdot A M^{2} \cdot A A_{1} = a^{3} {(1 - \frac{1}{\sqrt[]{2}})}^{2} = a^{3} (\frac{3}{2} - \sqrt[]{2}) . \end{matrix}

3. ábra

A 3. ábrán az

A C

átló és a

G G_{1}

él a nézőirány, itt a második kocka további

4

lapját látjuk ,,élben'', az első kockának pedig az

A B C D

lapját és ami ezzel párhuzamos. A fönt megállapított szimmetria alapján elég azt a gúlát tekintenünk, amely a

G F

lapon kívül esik. Alaplapja az előző nézet szerint a

B M Q

egyenlő szárú derékszögű háromszög, negyedik csúcsa

K

, a

B B_{1}

és

F F_{1}

élek közös felezőpontja. Az alap területe

M Q^{2} / 4 = a^{2} / 4

, a magasság

B K = a / 2

. Így a

4

egybevágó gúla térfogatának összege

\begin{matrix} 4 \cdot \frac{1}{3} \cdot \frac{a^{2}}{4} \cdot \frac{a}{2} = \frac{a^{3}}{6} . \end{matrix}

Számba vettük a levágásoknál a második kockának mind a

6

lapját. Az első kockából lemetszett részek térfogatának összege

\begin{matrix} a^{3} (\frac{3}{2} - \sqrt[]{2} + \frac{1}{6}) = a^{3} (\frac{5}{3} - \sqrt[]{2}), \end{matrix}

ennélfogva a két kocka közös részének térfogata

\begin{matrix} a^{3} (1 - \frac{5}{3} + \sqrt[]{2}) = a^{3} (\sqrt[]{2} - \frac{3}{2}) = a^{3} \cdot 0,748 \end{matrix}

térfogategység.

Megjegyzések. 1. A fenti leírás után önállóan is leírhatjuk a közös részt. A

2 \cdot 6 = 12

kockalap mindegyikéből egy-egy rész határolja. A

t

-re merőlegesen középen

4

téglalap (pl.

M N P Q

) egy hasábot határol, alapidoma

a

oldalú négyzet, magassága

M N = \sqrt[]{2} \cdot A M = a (\sqrt[]{2} - 1)

. Erre mindkét véglapján egy-egy négyoldalú gúla épül, magassága

a / 2

, fele annyi, mint a

B M Q

háromszög

M Q

-ra merőleges magassága. Így a térfogat ismét

\begin{matrix} V = a^{2} (M N + \frac{2}{3} \cdot \frac{a}{2}) = a^{3} (\sqrt[]{2} - \frac{2}{3}) . \end{matrix}

A maradéktest tengelyének hossza

2 \cdot 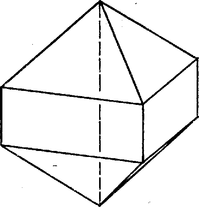O K = a \sqrt[]{2}

(4. ábra).

4. ábra

2. Ha a 2. és 3. ábrákat úgy állítjuk egymáshoz képest, hogy az

A C C_{1} A_{1}

metszetek élben látszó képei egy

g

egyenesbe essenek, akkor a két nézet tulajdonképpen az ábrázoló geometria elemeiben szokásos első és második kép. Méghozzá egymás tükrös képei egy a

g

-re merőleges képtengelyre, különben az egyes képeknek is két merőleges szimmetriatengelye van. Többen ilyen vetületpárból olvasták ki az

A B

és

F G

típusú élpárok metsződését, abból, hogy a két nézet látszólagos metszéspontjait összekötve, ez az egyenes párhuzamos

g

-vel, vagyis a két látszó kép ellenőrzi egymást, a metszés valóságos.
3. A bevezető számítás szerint

A M G ∢ = 60^{\circ}

. Vázoljuk ennek egy távolabbi kapcsolatát. A második kockát úgy is megkapjuk az elsőből, hogy

90^{\circ}

-kal elfordítjuk a

B B_{1}

és

D D_{1}

élek felezőpontjait összekötő

K K_{1}

,,éltengely'' körül. Ugyanilyen forgatást végezve az

A A_{1}

és

C C_{1}

-hez tartozó éltengely körül, ez a harmadik kocka ugyanolyan kölcsönös helyzetben lesz a másodikkal is, mint az elsővel, és a

3

kocka együttese többféle szimmetriával átvihető önmagába. Ebből értelmezhető a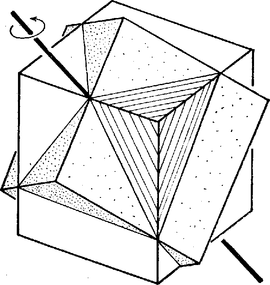

60^{\circ} = 180^{\circ} / 3

5. ábra