Feladat: F.2540 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bánkövi J. ,  Baross Á. ,  Beke T. ,  Bereczky Á. ,  Berszám F. ,  Biró J. ,  Blahota I. ,  Bodor Cs. ,  Bóna M. ,  Bortel L. ,  Csott R. ,  Cynolter G. ,  Drahos E. ,  Drasny G. ,  Grallert Ágnes ,  Gyuris V. ,  Habony Zs. ,  Hantosi Zsolt ,  Istanovszki M. ,  Janszky J. ,  Jedlovszky P. ,  Klug R. ,  Lengyel 24 Cs. ,  Ligeti Z. ,  Majoros L. ,  Makó B. ,  Mátrai K. ,  Olasz-Szabó M. ,  Pál G. ,  Rimányi R. ,  Szabó 149 T. ,  Szalay Gy. ,  Szederkényi Judit ,  Várkonyi V. ,  Vasy A. ,  Zaránd G. 
Füzet: 1986/március, 103 - 106. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Trigonometriai azonosságok, Magasságpont, Terület, felszín, Számtani-mértani egyenlőtlenségek, Szinusztétel alkalmazása, Szögfüggvények, síkgeometriai számítások, Ellenpélda, mint megoldási módszer a matematikában, Feladat
Hivatkozás(ok):Feladatok: 1985/szeptember: F.2540

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés. Jobban fejezzük ki a dolgozatok tartalmát, ,,műfaját'', ha a szokásos ‐és kissé sablonos ‐ ,,megoldás'' szó helyett ezúttal mást használunk. Mindig célszerű mérlegelni, hogy rokon értelmű szavak közül melyik a találóbb.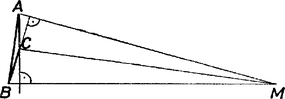
I. hozzászólás. A javaslat nem szab ki feltételt a háromszögre, így az egyaránt lehetne hegyes-, derék- és tompaszögű is. Viszont a derékszögű háromszögeket ,,kapásból'' kizárhatjuk, hiszen azokban M azonos a derékszög csúcsával, tehát valamelyik nevező 0. Továbbá ,,belső szemlélet'' útján látjuk, hogy ,,nagyon lapos'' háromszögekben M mindegyik csúcstól messzebb van, mint a megfelelő oldal (1. ábra), tehát (1) bal oldala az 1+1+1=3 értéket sem éri el. Egyszerű számpélda is mutatja, hogy (1) nem érvényes, ha γ=ACB∢=120∘ és CA=CB, pl. =1, amikor α=β=30∘, az MAB háromszög szabályos, és a bal oldal értéke 5/3<33 (2. ábra).

 
 
1. ábra
 

 
 
2. ábra
 

Megmutatjuk viszont, hogy (1) minden hegyesszögű háromszögre érvényes. Ilyenkor M a háromszög belsejében van, a háromszög területe egyenlő az MBC, MCA, MAB háromszögek területének összegével (3. ábra).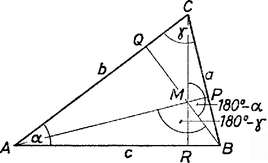
 
 
3. ábra
 


A területek 2-szeresét véve, a merőleges szárú szögek tétele alapján
cbsinα=MB⋅MCsin(180∘-α)+MC⋅MAsin(180∘-β)+MA⋅MBsin(180∘-γ).
Szorozzuk mindkét oldalt a-val, osszuk MA⋅MB⋅MC⋅sinα-val (ami ≠0) és alkalmazzuk a szinusztételt:
abcMA⋅MB⋅MC=aMA+bMB+cMC.(2)

A jobb oldal tagjai pozitívak, ezért a számtani és a mértani közepek közti egyenlőtlenség alapján
13(aMA+bMB+cMC)≧abcMA⋅MB⋅MC3,(3)
és a jobb oldalon ráismerünk (2) bal oldalának köbgyökére. Mivel kisebb számnak a köbe kisebb, (2) és (3) alapján
127(aMA+bMB+cMC)3≧aMA+bMB+cMC.
Másrészt nagyobb pozitív szám négyzetgyöke nagyobb, így (osztás után)
133(aMA+bMB+cMC)≧1,
ami ekvivalens az (1)-beli állítással. Ezt akartuk igazolni.
Ezek szerint a feladat állítását finomítani kellene, pl. így: ,,hegyesszögű háromszögekre igazoljuk az (1) egyenlőtlenséget''.
II. hozzászólás. Élesebben határozhatjuk meg (1) érvényességi körét, ha a szögekkel kapcsolatos értelmezést adunk a bal oldal hányadosaira. A jelöléseket úgy választjuk, hogy a≦b≦c legyen, így α≦β≦γ, tehát α és β mindenesetre hegyesszögek.
 
 
4. ábra
 

A CRB és ARM derékszögű háromszögek hasonlóságából
CBAM=aMA=CRAR=tgα,ugyanígybMB=tgβ
és ha γ<90∘ (I. eset, 3. ábra), akkor c/MC=tgγ. Ha pedig γ>90∘ (II. eset, 4. ábra), akkor az ABP, MCP háromszögpár hasonlóságából
cMC=ABMC=APMP=tgPMA∢=tg(180∘-ACB∢)=tg(α+β).
(ami egyébként tgγ abszolút értéke).
Ismeretes, hogy ‐ a derékszögű háromszögek kivételével ‐ minden háromszögben a szögek tangenseinek összege és szorzata egyenlő:
tgα+tgβ+tgγ=tgαtgβtgγ.

Az I. esetben mindhárom tangens pozitív, és fölismerjük, hogy a bal oldal az A számtani közepük 3-szorosa, a jobb oldal pedig a G mértani közepük köbe: 3A=G3. Ámde tudjuk, hogy A≧G, így A3≧G3=3A, ebből A≧3, ami azonos a kérdéses állítással, ha azt 3-mal osztjuk.
A II. esetben (1) így alakul
tgα+tgβ+tg(α+β)≧33,(4)
és akkor α+β<90∘, így a bal oldali tagok éppen növekvően vannak rendezve. Belátjuk, hogy a harmadik tag nagyobb, mint az első kettőnek az összege:
tg(α+β)=tgα+tgβ1-tgαtgβ>tgα+tgβ.(5)
Valóban, β<90∘-α és így 0<tgαtgβ<tgα⋅tg(90∘-α)=1, tehát a nevezőre teljesül
0<1-tgαtgβ<1.

Mármost (5) alapján minden olyan (tompaszögű) háromszög ellenpélda az állításra, amelyben
tgα+tgβ+tg(α+β)<2tg(α+β)<33,α+β<arctg332<69∘(≈68,948275∘),


vagyis amelyben γ>111∘ (radiánról mindjárt átszámítottuk fokra a szöget). Következő becslésünk alapján viszont olyan tompaszögű háromszögeket jellemezhetünk, amelyekre teljesül (1).
Bebizonyítjuk a következő egyenlőtlenséget:
tgα+tgβ≧2tgα+β2.(6)
Legyen röviden α+β=x, így β=x-α, felhasználjuk továbbá, hogy
tgx=2tgx21-tg2x2.(7)

A bal és a jobb oldal különbségét így alakítjuk:

tgα+tg(x-α)-2tgx2=tgα+tgx-tgα1+tgxtgα-2tgx2==tgx1+tgxtgα(tg2α+1-2tgx2tgx-2tgx2tgα).


Mivel a zárójelbeli tört (7) szerint 1-tg2x2, azért a zárójel(tgα-tgx2)2≧0, másrészt a kiemelt tényező is pozitív. Ezzel bebizonyítottuk (6)-ot és azt is látjuk, hogy egyenlőség csak α=x/2=β esetén áll be.
Ha tehát úgy választjuk (α+β)-t, hogy (4) helyén még az erősebb
2tgα+β2+tg(α+β)≧33
egyenlőtlenség is teljesüljön, akkor az ilyen háromszögekre érvényes az állítás. Táblázat használata nélkül belátható, hogy ez α+β≧75∘ (azaz γ≦105∘) esetén mindig teljesül, ui. tg75∘=2+3 és tg37,5∘=(3-2)(2+1), ezekkel a két oldal különbsége 2(6-2-1)>0, hiszen 6>(2+1)2=3+8, ‐ továbbá a tangensfüggvény a (0,90∘) intervallumban monoton nő.
Tehát azt kaptuk, hogy a feladat állítása mindig teljesül, ha a háromszög legnagyobb szöge legfeljebb 105∘ (és nem derékszög), és biztosan nem teljesül, ha a legnagyobb szög legalább 112∘.