Kezdőlap


Feladat:	F.2528	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh 961 Cs. , Bán Rita , Blahota I. , Bóna M. , Bortel L. , Csermely Ágnes , Cynolter Gábor , Deák CS. , Derzsi S. , Dinnyés Enikő , Edvi T. , Erdei Zs. , Fülöp T. , Grallert Ágnes , Hetyei Judit , Íjjas Cs. , Kónya Eszter , Licsik I. , Limbek Cs. , Németh-Buhin Á. , Olasz-Szabó M. , Pfeil T. , Pintér A. , Regős G. , Ribányi Á. , Róth E. , Sobor G. , Szigeti Z. , Tóth 728 F. , Török A. , Varga 135 L. , Varsányi Tünde
Füzet:	1985/november, 378 - 380. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Beírt kör, Hossz, kerület, Polinomok szorzattá alakítása, Prímtényezős felbontás, Feladat
Hivatkozás(ok):	Feladatok: 1985/április: F.2528

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Jelölje $R$ és $r$ rendre az adott sugarakat és $2 s$ a kerületet. Az adathármast szimmetrikusnak mondhatjuk abból a szempontból, hogy egyik oldal vagy szög sincs kitüntetve a többiekkel szemben. Ha tehát valahogyan kapnánk egy egyenletet pl. valamelyik oldalra, annak a további két oldalra éppúgy teljesülnie kellene, így legalább harmadfokúnak kellene lennie. Más kilátás hiányában ilyet keresünk.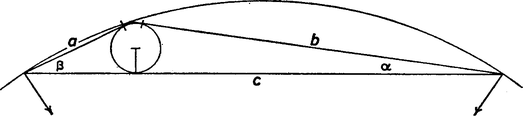

Ismeretesek a

4 R t = a b c

és

t = r s

összefüggések, ahol

t

a terület. Mindkettő ,,szimmetrikus''

a

b

c

-ben és ilyen a Heron-féle területképlet is:

t^{2} = s (s - a) (s - b) (s - c)

. Ez a három összefüggés elegendő lesz annak a harmadfokú egyenletnek a felírásához, amelynek a gyökei

a

b

c

. Ezek ismeretében térünk majd rá a szögek kiszámítására.
Az egyenlet gyöktényezős alakját kifejtjük:

\begin{matrix} (x - a) (x - b) (x - c) = x^{3} - (a + b + c) x^{2} + (a b + b c + a c) x - a b c = 0, \end{matrix}

itt máris ismerjük az első és a harmadik együtthatót:

a b c = 4 R t = 4 R r s

. A második együtthatót is megkapjuk a Heron-képlet kifejtéséből

\begin{matrix} t^{2} = r^{2} s^{2} = s (s^{3} - (a + b + c) s^{2} + (a b + b c + a c) s - a b c), \end{matrix}

ahonnan

\begin{matrix} a b + b c + c a = \frac{1}{s} (r^{2} s - s^{3} + 2 s^{3} + a b c) = r^{2} + s^{2} + 4 R r, \end{matrix}

tehát az egyenlet:

\begin{matrix} x^{3} - 2 s x^{2} + (r^{2} + s^{2} + 4 R r) x - 4 R r s = 0, \end{matrix}

számadatainkkal

\begin{matrix} x^{3} - 416 x^{2} + 51 568 x - 1 697 280 = 0. \end{matrix}

2. Próbáljuk meg, van-e egész gyöke az egyenletnek. Ez csak az

x

-től mentes tag osztója lehet, hiszen az első három tag osztható

x

-szel. Törzsszámhatványok szorzatára felbontva

1 697 280 = 2^{9} \cdot 3 \cdot 5 \cdot 13 \cdot 17

. Próbálkozzunk ennek

2^{5} = 32

és

2^{6} = 64

osztóival: Jelöljük az egyenlet bal oldalát

P (x)

-szel, így

P (32) = - 440 320 < 0

és

P (64) = + 161 280 > 0

. Ezek ellentétes előjelűek, másrészt

P (x)

folytonos függvény, ezért van

0

-helye a

(32,64)

intervallumban. Éspedig a

- 440

ezer és

+ 161

ezer ,,hibák'' nagyságviszonya alapján várhatóan közelebb a

64

-hez. Ilyen osztói az

x

-től mentes tagnak:

3 \cdot 17 = 51

és

2^{2} \cdot 13 = 52

. Valóban

P (52) = 0

, tehát

x_{1} = 52

.
A további két gyök összege:

x_{2} + x_{3} = x_{1} + x_{2} + x_{3} - 52 = 416 - 52 = 364

, szorzatuk:

x_{2} x_{3} = x_{1} x_{2} x_{3} : x_{1} = x_{1} x_{2} x_{3} : 2^{2} \cdot 13 = 2^{7} \cdot 3 \cdot 5 \cdot 17 = 32 640,

tehát a további két oldal a következő másodfokú egyenlet gyöke:

\begin{matrix} x^{2} - 364 x + 32 640 = 0, x_{2} = 160, x_{3} = 204. \end{matrix}

Tehát a háromszög oldalai

a = 52

b = 160

c = 204

. Ebben a háromszögben

R

r

és a kerület valóban egyenlő az előírt méretekkel.
3. Kiszámítjuk a két kisebb oldallal szemben fekvő szögeket, amelyek biztosan hegyesszögek:

\begin{matrix} sin α = \frac{a}{2 R} = \frac{52}{340}, sin β = \frac{b}{2 R} = \frac{160}{340}, \\ α = 8^{\circ} 47,8', β = 28^{\circ} 4,4' végül γ = 143^{\circ} 7,8' . \end{matrix}

Megjegyzés. Kisebb számokkal dolgozhatunk, ha

a

b

c

helyett a beírt kör

s - a

s - b

s - c

érintőszakaszaira írunk fel harmadfokú egyenletet. Ezekre a gyökök szimmetrikus kifejezései:

\begin{matrix} (s - a) + (s - b) + (s - c) = s, \\ (s - a) (s - b) + (s - b) (s - c) + (s - a) (s - c) = 3 s^{2} - s \cdot 4 s + (a b + a c + b c) = r^{2} + 4 R r, \\ (s - a) (s - b) (s - c) = t^{2} / s = r^{2} s, \end{matrix}

ezek tehát a következő egyenlet gyökei:

\begin{matrix} z^{3} - s z^{2} + (r^{2} + 4 R r) z - r^{2} s = 0. \end{matrix}

Számadatainkkal

z^{3} - 208 z^{2} + 8304 z - 29 952 = 0

, és mivel

2 s

páros szám, ugyanolyan eséllyel remélhetjük, hogy

s - a

...

is egészek, mint a föntebbi próbálkozásban. Innen

z_{1} = 156

z_{2} = 48

z_{3} = 4

útján

a = 208 - 156 = 52

-re és tovább az előbbi eredményekre jutunk.