Kezdőlap


Feladat:	F.2527	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bán Rita , Bereczky Á. , Blahota I. , Bóna M. , Bortel L. , Csermely Ágnes , Cynolter G. , Deák CS. , Dinnyés Enikő , Edvi T. , Erdei Zs. , Fülöp T. , Grallert Ágnes , Hajdú G. , Hetényi Zs. , Hetyei Judit , Hornok S. , Íjjas Cs. , Kocsis 443 Katalin , Kónya Eszter , Licsik I. , Ligeti Z. , Limbek Cs. , Németh-Buhin Á. , Nyikes T. , Olasz-Szabó M. , Pfeil T. , Pintér A. , Regős G. , Ribényi Á. , Szigeti Z. , Varga 135 L. , Zaránd G.
Füzet:	1985/november, 376 - 378. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Terület, felszín, Számtani sorozat, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1985/április: F.2527

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A háromszögekben szokásos jelölésekkel a szögfelező osztási aránya alapján

\begin{matrix} B D = a \cdot \frac{c}{b + c}, B F = c \cdot \frac{a}{a + b}, \end{matrix}

így a

B D F

háromszög területe:

\begin{matrix} \frac{1}{2} B D \cdot B F \cdot sin β = \frac{a^{2} c^{2} sin β}{2 (a + b) (b + c)}, \end{matrix}

és a

B D F

A B C

háromszögek területének aránya:

\begin{matrix} \frac{a^{2} c^{2} sin β}{2 (a + b) (b + c)} : \frac{a c sin β}{2} = \frac{a c}{(a + b) (b + c)} . \end{matrix}

(1)

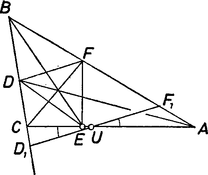Ugyanígy az

A E F

és

C D E

háromszögek területének az eredeti háromszög területéhez való aránya

\begin{matrix} \frac{c b}{(c + a) (a + b)}, \frac{b a}{(b + c) (c + a)}, \end{matrix}

ennélfogva a

D E F

A B C

területek aránya, mindjárt tovább alakítva

\begin{matrix} 1 - (\frac{a c}{(a + b) (b + c)} + \frac{c b}{(c + a) (a + b)} + \frac{b a}{(b + c) (c + a)}) = \frac{2 a b c}{(a + b) (b + c) (c + a)} \end{matrix}

(2)

(egyetlen nevező sem válhat zérussá).
Mármost a kívánt egyenlőség akkor és csak akkor teljesül, ha (2) és (1) kifejezések egyenlők. Ebből egyszerűsítéssel

\begin{matrix} \frac{2 b}{c + a} = 1, azaz ha b = \frac{a + c}{2} . \end{matrix}

Szavakban: ha a követelményben kitüntetett szerepet játszó

B

csúccsal szemben fekvő

b

oldal a másik kettőnek számtani közepe, más szóval, ha az

a

b

c

oldalak ebben a sorrendben számtani sorozatot alkotnak.

Csermely Ágnes (Veszprém, Lovassy L. Gimn., IV. o. t.)

A következő megoldásban a számítások mellett némi geometriai szemlélődés is van.

II. megoldás. Közös

D F

alapjukra tekintettel a kérdéses háromszögek területe akkor és csak akkor egyenlő, ha a

B

E

pontoknak a

D F

egyenestől mért távolságai egyenlők. Ez a feltétel ekvivalens a következővel: párhuzamost húzva

E

-n át

D F

-fel, ez a

B C

B A

félegyeneseket azokban a

D_{1}

F_{1}

pontokban metszi, amelyekre

B D_{1} = 2 \cdot B D

ill.

B F_{1} = 2 \cdot B F

.
Tekintsük tehát ezt a két pontot, továbbá a

D_{1} F_{1}

egyenesnek

A C

-vel való

U

metszéspontját, és keressük annak a feltételét, hogy

U

essék egybe

E

-vel. Egyelőre föltesszük, hogy

D_{1}

nem azonos

C

-vel ‐ amiből nyilvánvalóan

A B \neq A C

‐ és

F_{1}

nem azonos

A

-val, tehát

C B \neq B A

. Az

U

pont akkor és csak akkor keletkezik

C

és

A

között, ha

D_{1}

és

F_{1}

A C

egyenes két különböző partján fekszik.
1. Válasszuk úgy a betűzést, hogy

B D_{1} = 2 B D > A C

, és

B F_{1} = 2 B F < B A

legyen. Ekkor

B D > C D

miatt ‐ a szögfelező osztásaránya alapján ‐

B A > C A

, másrészt

B F < A F

folytán

B C < C A

, tehát

C A

a nagyságra nézve középső oldal.
Az

U C D_{1}

és

U A F_{1}

háromszögekből

\begin{matrix} sin C U D_{1} ∢ = \frac{C D_{1}}{C U} sin C D_{1} U ∢ = \frac{C D_{1}}{C U} sin B D F ∢, \end{matrix}

és

\begin{matrix} sin C U D_{1} ∢ = sin A U F_{1} ∢ = \frac{A F_{1}}{A U} sin A F_{1} U ∢ = \frac{A F_{1}}{A U} sin B F D ∢, \end{matrix}

tehát hányadosuk

\begin{matrix} \frac{C D_{1}}{A F_{1}} \cdot \frac{A U}{C U} \cdot \frac{sin B D F ∢}{sin B F D ∢} = 1. \end{matrix}

(3)

Ámde ismét az osztásarány alapján

\begin{matrix} \frac{sin B D F ∢}{sin B F D ∢} = \frac{B F}{B D} = \frac{a c}{a + b} : \frac{c a}{c + b} = \frac{b + c}{b + a}, \end{matrix}

továbbá szerkesztésünknél fogva

\begin{matrix} C D_{1} & = 2 B D - B C = \frac{2 a c}{b + c} - a = \frac{a (c - b)}{b + c}, & (c > b), \\ A F_{1} & = B A - 2 B F = c - \frac{2 a c}{a + b} = \frac{c (b - a)}{a + b} & (b > a) . \end{matrix}

Ezeket (3)-ba beírva, rendezés után

\begin{matrix} \frac{A U}{C U} = \frac{c}{a} \cdot \frac{b - a}{c - b} . \end{matrix}

(4)

A feladat föltételei szerint pedig

\begin{matrix} \frac{A E}{C E} = \frac{A B}{C B} = \frac{c}{a} . \end{matrix}

(5)

Ha egy

X

pont az

A C

szakaszon

A

-tól

C

-ig halad, akkor az

A X : X C

arány minden pozitív értéket fölvesz, éspedig csak egyszer, hiszen

A X

monoton nő és

X C

monoton fogy. Eszerint

U

akkor és csak akkor esik egybe

E

-vel, ha (4) és (5) összehasonlításából

\begin{matrix} \frac{b - a}{c - b} = 1, \end{matrix}

vagyis az

a

b

c

(különbözőknek tekintett) oldalhosszak számtani sorozatot alkotnak.
2. Ha

D_{1}

és

F_{1}

egyike azonos volna

C

-vel, ill.

A

-val, a másik viszont nem ‐ pl.

B C = 2 B D

és

B A \neq 2 B F

‐, akkor a

D F

egyenes

B

-ből

2 : 1

arányban nagyított képének egyetlen közös pontja van

C A

-val, tehát

E

és

B

különböző távolságra vannak

D F

-től, lehetetlen tehát, hogy a

B D F

és

E D F

háromszögek területe egyenlő legyen.
Ha viszont

D_{1}

azonos

C

-vel és

F_{1}

azonos

A

-val, akkor nyilvánvalóan egyenlő a két terület. Ez akkor és csak akkor következik be, ha

D

és

F

egyúttal oldalfelező pontok is, tehát

A B = A C

, valamint

C B = C A

, vagyis a háromszög szabályos. Ekkor elfajultan teljesül, hogy

a

b

c

számtani sorozat, tehát a fent kapott szükséges és elegendő feltételhez nincs hozzátenni valónk.

(B. T.)