Kezdőlap


Feladat:	F.2515	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Domokos Mátyás , Makay Géza
Füzet:	1985/október, 300 - 303. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Terület, felszín, Párhuzamos szelők tétele, Párhuzamos szelők tételének megfordítása, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1985/február: F.2515

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. A válasz: igen, fel lehet osztani. Sőt mindjárt többet is követelhetünk: egybevágó részekre osztjuk az $A B C D$ parallelogrammát. Ismételten támaszkodunk a következő segédtételre: az adott $A B$ szakasz megfelezhető egyetlen (egyélű, hosszúságmérő beosztást nem tartalmazó, az $A B$ szakasz hosszát kissé meghaladó) egyenes vonalzó felhasználásával, ha adott vele párhuzamosan egy $e$ egyenes ‐ mint esetünkben a $C D$ oldal egyenese.
2. Felvéve az $A D$ oldal $D$ -n túli meghosszabbításán egy $P$ pontot, a $P B$ és $D C$ egyenesek metszéspontját $Q$ -val, az $A B Q D$ trapéz átlóinak metszéspontját $R$ -rel jelölve azt állítjuk, hogy a $P R$ egyenes kimetszi az $A B$ szakasz $F$ felezőpontját (1. ábra).

1. ábra

Bizonyításul gondoljuk berajzolva az

R

-en átmenő,

e

-vel párhuzamos egyenest, és jelöljük az

A D

B Q

szárral való metszéspontját

T_{1}

-gyel, ill.

T_{2}

-vel Ekkor

R T_{1}

és

R T_{2}

aránya ‐ a párhuzamos szelők tétele alapján ‐ megadja

F A

és

F B

arányát, hiszen

\begin{matrix} R T_{1} = \frac{R P}{F P} \cdot F A és R T_{2} = \frac{R P}{F P} \cdot F B . \end{matrix}

Másrészt ugyanezt a tételt egymás után a

D

-n,

R

-en,

Q

-n átmenő 2‐2 egyenesre alkalmazva.

\begin{matrix} \frac{R T_{1}}{B A} = \frac{R D}{B D} = \frac{R Q}{A Q} = \frac{R T_{2}}{A B}, \end{matrix}

ennélfogva

R T_{1} = R T_{2}

, tehát

F A = F B

, amint állítottuk.
Segédtételünket ismételgetve kijelöljük az

F A

és

F B

szakaszok

G_{1}

és

G_{2}

felezőpontját (

Q

szerepét az a

Q_{1}

veszi át, ahol

P F

metszi

D C

-t), majd az egymással egyenlő

F G_{1}

F G_{2}

B G_{2}

szakaszok

H_{1}

H_{2}

, ill.

H_{3}

felezőpontját. Ekkor a

H_{1} B

szakasz

5

egyenlő részre van felosztva, és az osztópontok felhasználásával

5

egyenlő részre oszthatjuk a

D C

szakaszt: legyen

D H_{1}

és

C B

metszéspontja

U

, ekkor a keresett

D_{1}

D_{2}

D_{3}

D_{4}

osztópontokat egymás után az

U F

U H_{2}

U G_{2}

U H_{2}

egyenesek metszik ki.
3. Ezen a ponton ‐ logikai szempontból ‐ a következő folytatás a legegyszerűbb: ugyanígy megszerkesztjük az

A B

szakaszt

5

egyenlő részre felosztó

A_{1}

A_{2}

A_{3}

A_{4}

pontokat, és akkor az

A_{1} D_{1}

A_{2} D_{2}

A_{3} D_{3}

A_{4} D_{4}

szakaszok nyilvánvalóan

5

egybevágó részre osztják

A B C D

-t, tehát a területeik egyenlőek.
Szerkesztésünk tetszőleges

n (> 1)

természetes szám esetén használható, addig ismételjük az

A B

-n keletkező részek felezgetését,

A B / 2^{k}

megszerkesztését (

k

természetes szám), míg

2^{k} > n

lesz

Megjegyzések. 1. Ez a megoldás egy másik tekintetben is megemelte a feladatbeli korlátozást: a segédtételt csak az eredeti megfogalmazásában használta fel.
2. A fönti megoldás befejezése csupán ,,logikailag'' egyszerű, amikor valaki csak elmondással (,,szájjal'') szerkeszt. Számlálja csak végig az olvasó, hány egyenest rajzol be, míg megkapja a

D_{4}

osztópontot, ekkor még egyszer annyira van szükség

A_{4}

-ig.
Gyakorlatilag viszont rövidebb a következő: az

A C

átló a már meglevő

B D

-ből kimetszi a parallelogramma

O

középpontját, és ekkor

D_{1} O

...

D_{4} O

kimetszi

A_{4}

-et,

...

A_{1}

-et.

II. megoldás. A következő megoldásban a segédtétel megfordítását használjuk fel: ismerve egy szakasz végpontjait és a felezőpontját, a sík tetszőleges pontján át megszerkeszthető a szakasszal párhuzamos egyenes.
A bizonyítást az 1. ábra

A

B

és

F

, valamint

D

pontjára mondjuk el, de majd máshogyan alkalmazzuk esetünkre. A lépések: összekötjük az

A D

egyenes tetszőleges

P

pontját

B

-vel és

F

-fel, továbbá

D

-t is

B

-vel, ez az egyenes

P F

-ből kimetszi

R

-et, és ekkor az

A R

B P

egyenesek

Q

metszéspontja ‐ ami nyilván nem azonos

D

-vel ‐ rajta van a keresett

e

párhuzamoson.
A fentiek mintájára

5

egyenlő hosszú, egymás után csatlakozó szakaszt állítunk elő ‐ de a parallelogramma egyik átlójával párhuzamos egyenesen. Ezek alapján

5

egyenlő részre oszthatjuk a parallelogramma megfelelő átlószakaszát, és az osztópontokon át bármelyik oldallal párhuzamosan húzott egyenesekkel ismét

5

egybevágó részt kaphatunk.

2. ábra

A 2. ábrán az átlók metszéspontja

F

. Csak a

D

-n átmenő,

A C

-vel párhuzamos egyenes szerkesztését vázoltuk (

P

R

Q

pontok). Ugyanígy kapható a megfelelő átlóval párhuzamos egyenes az

A

és

B

csúcson át ‐ a metszéspontok

J

és

K

‐, majd a

J F

és

K F

egyenes kimetszi a

J^{*}

K^{*}

tükörképeket, továbbá a

B K

egyenes

D A

-ból

M

-et,

D C

-ből

N

-et, és ekkor

M K = K B = B J^{*} = J^{*} N

. Még egy párhuzamost szerkesztünk, pl.

K^{*}

-on át

A B

-vel, ennek

B K

-n levő pontja legyen

N_{1}

, így

N N_{1}

az ötödik egyező szakasz.
Legyen végül

N_{1} C

és

A D

metszéspontja

S

, ezt véve vetítési középpontnak, megkapjuk az

A C

-t

5

egyenlő részre osztó pontokat. Ezeken át megszerkesztve vagy az

A B

-vel, vagy az

A D

-vel párhuzamos egyeneseket, ezek mindjárt a kívánt osztóvonalak lesznek.

Megjegyzések. 1. A 2. ábra szerint pl. az

A B

egyenesen is könnyen kaphatunk

5

egymás után csatlakozó, egyenlő hosszú szakaszt ‐ és a hálózat bővítésével tetszőleges számút is. Ha ennek alapján a

J J^{*}

középvonalnak a parallelogrammába eső szakaszát osztjuk

5

egyenlő részre, így különböző alakú, nem egybevágó részekre való fölosztást is mutathatunk: a 3. ábra szerinti részek ─ ha mindegyik valóban trapéz ‐ középvonalaik alapján egyenlő területűek.

3. ábra

2. Felszabadulva a részek egybevágóságának magunkra vállalt ,,nyűgétől'' ‐ ettől a ,,munkahipotézistől'' ‐ a 4. ábrán további két megoldást vázoltunk különböző alakú részeket is tartalmazó felosztásra. Az első azonban kivételesen csupa egybevágó részből is állhat, ha

A B : A D = 5 : 2

4. ábra

III. megoldás. Mintának vesszük azt az ismert szerkesztést, ahogyan adott négyzetet át lehet darabolni

5

egyező oldalú négyzetbe (5. ábra): oldalainak felezőpontjait ciklikusan összekötve a következő oldal végpontjával, és a

9

rész közül a derékszögű trapézokat egyesítve a szomszédos derékszögű háromszögek egyikével. A szomszéd kétféle megválasztási lehetősége folytán az újra egyesített részek közös alakja háromszög vagy négyszög lehet.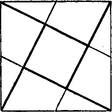

5. ábra

A feldarabolt négyzetnek bármely síkon való, párhuzamos vetítéssel készített képén ugyancsak egyenlőek a területek (csak a kép síkja ne álljon merőlegesen a négyzet síkjára), mert ilyen vetítés mellett a kép és az eredeti területeinek aránya a síkok hajlásszögének koszinuszával egyenlő.
Ez a felosztás végső soron az

5 = 1^{2} + 2^{2}

egyenlőségen alapul. Mégsem az

5

-ös szám az egyetlen ilyen, eljárhatunk hasonlóan a

10 = 1^{2} + 3^{2}

egyenlőség alapján is, 2‐2 kis tartományt egybefoglalva (6. ábra).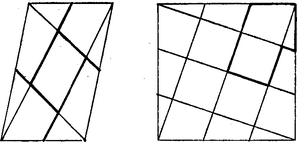

6. ábra

Mindezek az osztóvonalak a föntiek szerint megszerkeszthetők egyetlen egyenes vonalzóval.

Megjegyzés. Számos dolgozat felsorolta a felhasznált forrásokat. Legtöbbször szerepeltek: P. O. Sklarszkij ‐ N. N. Csencov ‐ I. M. Jaglom: Válogatott feladatok és tételek stb. Geom. I. (Planimetria) 65/d feladat; H. Dörrie. A diadalmas matematika 184. old.