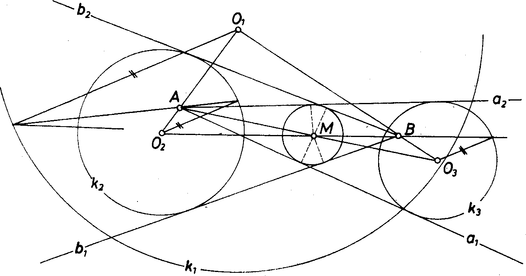Kezdőlap


Feladat:	F.2503	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balázsi Edina , Balogh 961 Cs. , Bán Rita , Blahota I. , Bóna M. , Boros Z. , Cynolter G. , Dinnyés Enikő , Domokos M. , Fülöp T. , Hetyei Judit , Íjjas Cs. , Kónya Eszter , Kovács 671 S. , Menyhárt I. , Németh-Buhin Á. , Pálmai L. , Pfeil T. , Regős G. , Szigeti Z. , Varga 135 L.
Füzet:	1985/május, 205 - 208. oldal		PDF \| MathML
Témakör(ök):	Menelaosz-tétel, Feladat
Hivatkozás(ok):	Feladatok: 1984/december: F.2503

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a $k_{i}$ kör középpontja $O_{i}$ $(i = 1, 2, 3)$ , a két kör közös külső érintőinek metszéspontja (azaz külső hasonlósági pontjuk) a $k_{1},$ $k_{2}$ körpár esetére $A$ , a $k_{1}$ , $k_{3}$ esetére $B$ , továbbá az $A$ -ból $k_{3}$ -hoz húzott érintők $a_{1}$ és $a_{2}$ , a $B$ -ből $k_{2}$ -höz húzott érintők $b_{1}$ és $b_{2}$ . Az $A$ , $B$ pontok létezését a feladat föltevései biztosítják, és azt is, hogy az $O_{i}$ pontok az $A B$ egyenes egyik partján vannak. Föltesszük azt is, hogy $A$ kívül van $k_{3}$ -on és $B$ kívül van $k_{2}$ -n, különben nem volna bizonyítanivalónk.

1. ábra

1. Az

O_{i}

középpontok általában nincsenek egy egyenesen, ekkor

A

és

B

különbözők. Először egy ilyen helyzetet tekintünk, bizonyításunkat az 1. ábrán látható helyzethez kapcsoljuk.
Az állítás szerinti kör középpontjaként csak az

a_{1}, a_{2},

valamint

b_{1}, b_{2}

érintőpár közti szögek egyik-egyik felezőjének

M

metszéspontja jöhet szóba. Emiatt

M

körül rajzolható olyan kör, amely érinti az

a_{1}, a_{2}

egyenespárt és olyan is, amely a

b_{1}, b_{2}

párt érinti. Legyen a sugaruk

ϱ_{a}

, ill.

ϱ_{b}

, a feladat állítása azt jelenti, hogy ezek egyenlők. Ezt akarjuk megmutatni az ábra

M

pontja esetére.
Alkalmazzuk Menelaosz tételét ^{$^{*}$} az

O_{1} O_{3} A

háromszögre és az

O_{2} B

átmetsző egyenesre, amely

M

-ben metszi az

O_{3} A

oldalegyenest:

\begin{matrix} \frac{A O_{2}}{O_{2} O_{1}} \cdot \frac{O_{1} B}{B O_{3}} \cdot \frac{O_{3} M}{M A} = - 1. \end{matrix}

Itt mindegyik szakasz egy körközéppontnak egy hasonlósági középponttól való távolsága vagy pedig két ilyen távolság különbsége, ennélfogva az arányok kifejezhetők a megfelelő körsugarakkal. Az irányokat is figyelembe véve

\begin{matrix} \frac{A O_{2}}{O_{2} O_{1}} = \frac{A O_{2}}{A O_{1} - A O_{2}} = \frac{r_{2}}{r_{1} - r_{2}}, \\ \frac{O_{1} B}{B O_{3}} = - \frac{B O_{1}}{B O_{3}} = - \frac{r_{1}}{r_{3}}, \\ \frac{O_{3} M}{M A} = \frac{M O_{3}}{A M} = \frac{A O_{3} - A M}{A M} = \frac{r_{3}}{ϱ_{a}} - 1, \end{matrix}

A

centrumra nézve ugyanis a

ϱ_{a}

sugarú kör van a

k_{3}

-hoz hasonló helyzetben.
Ezeket beírva

\begin{matrix} (\frac{r_{2}}{r_{1} - r_{2}}) \cdot (- \frac{r_{1}}{r_{3}}) \cdot (\frac{r_{3}}{ϱ_{a}} - 1) = - 1, \end{matrix}

amiből

\begin{matrix} ϱ_{a} = \frac{r_{1} r_{2} r_{3}}{r_{1} (r_{2} + r_{3}) - r_{2} r_{3}} . \end{matrix}

Ugyanilyen gondolatmenettel számíthatnánk a

ϱ_{b}

sugarat, abban azt kellene kihasználnunk, hogy a

ϱ_{b}

és

r_{2}

sugarú körök egymás megfelelői a

B

centrumú homotéciában. Az

O_{1} O_{2} B

háromszögre és az

O_{3} A

egyenesre alkalmaznánk Menelaosz tételét. Ez azonban csak a szerepek tükrözése lenne, egymás helyére lépnek

O_{2}

és

O_{3}

, tehát

r_{2}

és

r_{3}

, másrészt

A

helyére

B

, vagyis a

k_{1}, k_{2}

körpár centruma helyére a

k_{1}, k_{3}

körpár centruma. Mindkét változás azt jelenti, hogy

ϱ_{b}

értékét

ϱ_{a}

képletéből a

2

-es és

3

-as indexek fölcserélésével kaphatnánk.
Ámde a képletben

r_{2}

és

r_{3}

‐ mindhárom előfordulásukban ‐ szimmetrikus szerepet visznek, szorzatuk, ill. összegük szerepel, ennélfogva

ϱ_{a} = ϱ_{b}

. Ezzel bebizonyítottuk az állítást és a sugár kívánt kifejezését is megadtuk.

2. Ha

O_{1}, O_{2}

és

O_{3}

egy

t

egyenesen van, akkor előfordulhat, hogy

A

és

B

egybeesnek. Ilyen esetben a három kör két közös érintője vinné a feltételben szereplő

4

érintő szerepét; az állítás semmitmondó.
Ha

A

és

B

különbözők, ugyancsak

t

pontjai, akkor az

a_{1}, a_{2}

és

b_{1}, b_{2}

érintőpárok elemei egymás tükörképei

t

-re, deltoidot alkotnak, az állítás helyessége nyilvánvaló (2. ábra). A sugár képlete az

M

körre érvényes.

2. ábra

Megjegyzések. 1. Ha nemcsak a bizonyításban használjuk ki, hogy a közös külső érintők metszéspontja a körpár külső hasonlósági pontja, hanem mindjárt ezt mondjuk a feltételben, akkor az állítást többféle módon is kiterjeszthetjük. Tulajdonképpen egy tételcsalád erősen korlátozott speciális esetével állunk szemben. Érthető ez abból, hogy versenyfeladatról van szó, ilyenkor több okból is szokásos a témát erősebb feltételekkel mintegy ,,megnyirbálni'', csak az ,,oroszlánkörmeit'' említeni. Egyik ok, hogy a többi feladatra is maradjon idejük a versenyzőknek; egy másik, hogy ‐ akiknek van ráadás-mondanivalójuk ‐ bemutathassák az elemzésben, diszkutálásban való képességeiket, jártasságukat. ‐ Természetesen itt is csak néhány lehetőség felvillantására van hely.

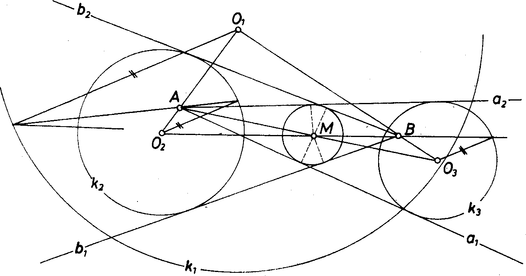3. ábra

Nem használtuk ki, hogy köreink páronként egymáson kívül állnak, pl. hogy

O_{1} O_{2} > r_{1} + r_{2}

, hiszen az állításbeli kör sugarának kifejezésében nem szerepelnek a centrumok közti távolságok. Rögzítve az

r_{1}, r_{2}, r_{3}

sugarak hosszát, a körök minden szóba jövő helyzetében ugyanakkora a negyedik kör sugara.
Külső hasonlósági pont akkor is létezik, ha pl.

k_{2}

tartalmazza

k_{1}

-et (!); ott futnak össze a párhuzamos és egyirányú sugarak végpontjait összekötő egyenesek, ha

r_{1} \neq r_{2}

. Más fogalmazással az

r_{1} = r_{2}

esetről is van mondanivaló. De érvényesek hasonló állítások belső hasonlósági pontok esetében is, vagyis ha párhuzamos és ellentétes irányú sugarak végpontjai révén származtatjuk az

A, B

pontokat.
Ezt viszont hozzá kell tenni a bizonyításhoz: 1. ábránkkal a ,,legkézenfekvőbb''

M

pontra szorítkoztunk, az

A O_{3}

és

B O_{2}

szögfelező szakaszok közös pontjára. Kihasználtuk a számításban, hogy

O_{2} O_{1} = A O_{1} - A O_{2}

és

M O_{3} = A O_{3} - A M

. Az

a_{1}, a_{2}

, valamint

b_{1}, b_{2}

érintőpárok közti 2-2 szögfelező

4

metszéspontja közül csak erre az egyre érvényes a számítás és az állítás.
A 2. ábrán a szimmetria folytán adódó

M^{*}

közepű kör sugara már a középpontok helyzetétől is függ.
2. Többen azzal a ,,kúpos'' eljárással bizonyították a feladat állítását, amellyel

3

kör

6

külső és belső hasonlósági pontjáról szokás bizonyítani, hogy alkalmasan véve közülük

3

-at, ezek egy egyenesre illeszkednek. A sugár kiszámítása viszont többnyire elmaradt.

^{$^{*}$}Bizonyítását lásd az F. 2497. feladat megoldásában. KÖMAL, 1985. évi májusi szám, 198. oldal.