Kezdőlap


Feladat:	F.2463	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1984/november, 375 - 376. oldal		PDF \| MathML
Témakör(ök):	Ellipszis egyenlete, Terület, felszín, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1984/február: F.2463

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$a)$ az $M B F$ háromszög $B F$ oldala rögzített, ezért területe akkor lesz legnagyobb, amikor a $B F$ -hez tartozó magassága a legnagyobb, azaz $M$ legtávolabb van $B F$ -től. Legyen az $e$ egyenes az $A B$ ívnek $B F$ -fel párhuzamos érintője, és ezen az érintési pont $M_{1}$ . Ekkor az ellipszisnek csak $e$ egyik partján van pontja, azon, amelyiken $B$ is van. Másrészt a $B F$ és $e$ egyenesek közti síksáv minden pontja legföljebb akkora távolságra van $B F$ -től, mint $e$ , illetve maga az $M_{1}$ pont.

A B

ellipszisív teljes egészében a síksávban van, illetve

M_{1}

és

B

a sávot határoló

e

, ill.

F B

egyenesen, ezért éppen

M_{1}

a keresett pont, vagyis az ellipszis

B F

-fel párhuzamos érintői közül az

F

-hez közelebbinek az érintési pontja.

b)

Ha helyzet szerint adottnak vesszük az

A

B

F

pontokat, akkor meg is szerkeszthetjük

M

-et, felhasználva azt, hogy az ellipszis legismertebb (,,vezérsugaras") definíciója egyenértékű a következővel. Ha adott a

2 a

hosszúság és az

F

F_{1}

pontok, amelyekre

F F_{1} < 2 a

, akkor az ellipszis azon körök középpontjainak mértani helye (tetszőleges, az

F F_{1}

egyenesen átmenő síkban), amelyek érintik az

F_{1}

körüli,

2 a

sugarú

k

kört, és átmennek az

F

ponton (belső érintkezés, ui.

F

k

belsejében van).
Valóban, ha a

P

középpontú

k'

kör átmegy

F

-en, és

E

-ben érinti

k

-t, akkor

E

F_{1} P

szakasz

P

-n túli meghosszabbításán van, és

P E = P F

miatt

P F_{1} + P = F_{1} E = 2 a

, állandó. (

E

-n az ábra

E^{*}

pontja értendő.)
A

k

-n tetszőlegesen megválasztott

E

ponthoz tartozó

P

-t az

F E

szakasz

m

felező merőlegese metszi ki

F_{1} E

-ből. Továbbá

m

éppen az ellipszis

P

-beli érintője, mert a

P

-től különböző bármely

Q

pontjára is fennáll

Q E = Q F

, de ekkor a

Q F_{1} E

valódi háromszög révén

\begin{matrix} Q F_{1} + Q F = Q F_{1} + Q E > F_{1} E = 2 a, \end{matrix}

tehát

Q

az ellipszisre nézve külső pont.
A mi esetünkben

m

iránya az adott, párhuzamosnak akarjuk

B F

-fel, következésképpen

F E

-t merőlegesen kell felvennünk

B F

-re. A szerkesztés tehát a következő: az

A F

egyenesre merőlegesen vetítjük

B

-t, ‐ ekkor az

O

vetületre az adott pontok definíciója alapján

O A = F B = a

‐,

F

-nek

O

-ra való

F_{1}

tükörképe körül megrajzoljuk

k

-t, és ezt metsszük az

F

-ben

F B

-re állított merőlegessel

E

-ben (ez az

F

-hez közelebbi metszéspont), ebből a föntiek szerint kapjuk

M

-et.

Megjegyzések. 1. Megszerkeszthető

M

abból is, hogy az ellipszis az

O

körüli,

O A

sugarú körnek a képe abban a merőleges affinitásban, amelynek tengelye az

O A

egyenes, és

B

annak a

B^{*}

pontnak a megfelelője, amelyre

O B^{*} ⊥ O A

és

O B^{*} = O A

. Ekkor

F B

megfelelője a kör rendszerében az

F B^{*}

egyenes, és ‐ mivel az affinitás párhuzamos egyeneseket párhuzamos egyenesekbe visz át ‐, úgy jutunk közelebb célunkhoz, hogy megszerkesztjük a körhöz az

F B^{*}

-gal párhuzamos érintőt. Pontosabban mondva: elég gondolni erre az érintőre, hiszen nekünk elég az

M^{*}

érintési pontja, ezt pedig kimetszi (a körből) az

O

-ból

F B^{*}

-re állított merőleges, természetesen az

F

-hez közelebbi metszéspontot véve. Végül

M

M^{*}

megfelelője az ellipszis rendszerében (vagyis pl.

B^{*} M^{*}

és

B M

A F

egyenesen metszik egymást).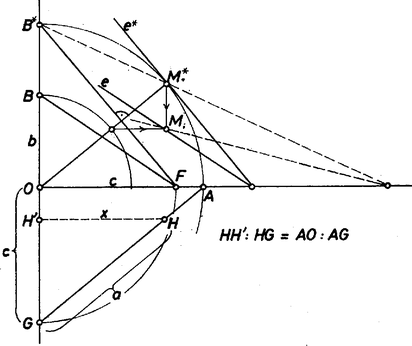

2. Többen koordinátageometriai segítséggel határozták meg

M

-et abból, hogy ‐ az ellipszis szokásos elhelyezése és betűzése mellett ‐ a

B F

egyenes iránytangense

(- b / c)

. Az ellipszis "felső'' ívének egyenlete

y = (b / a) \sqrt[]{a^{2} - x^{2}}

, érintőjének iránytangense deriválással

\begin{matrix} - \frac{b x}{\sqrt[]{a^{2} - x^{2}}} (hacsak x \neq \pm a) . \end{matrix}

A kettő egyenlő, ha

x / a = a / \sqrt[]{a^{2} + c^{2}}

.
A szerkesztés: elfordítjuk derékszöggel

F

-et

O

körül

G

-be, a

G A

félegyenesre rámérjük a

G H = a = B F

szakaszt, ekkor

H

abszcisszája megadja

M

abszcisszáját. (A "

2

-körös eljárással'' kaphatjuk

M

-et.)