Kezdőlap


Feladat:	F.2462	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Badics T. , Bóna M. , Bujdosó L. , Hegedűs P. , Ispány Márton , Katona Gy. , Ladányi L. , Sárközy G. , Simon P. , Somogyi Á. , Varga K.
Füzet:	1984/november, 371 - 375. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Háromszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1984/február: F.2462

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tekintsük a feladatot megoldottnak, vagyis az $X$ , $Y$ pontpárra teljesül a feladat minden követelménye (1. ábra).

1. ábra

Forgassuk az

A C Y

háromszöget az

A

csúcsa körül abba az

A C' Y'

helyzetbe, amelyben

C'

A B

félegyenesen van, majd nyújtsuk (ill, zsugorítsuk) ugyancsak az

A

centrumból

λ = A B / A C

arányban az

A C'' Y''

helyzetbe. Ezáltal

C''

azonos lesz

B

-vel, egyszersmind

Y''

azonos lesz

X

-szel. Valóban, a forgatás miatt (az egyenlőségekbe a forgási irányokat is beleértve)

\begin{matrix} Y'' A C'' ∢ = Y' A C' ∢ = Y A C ∢ = X A B ∢ = X A C'' ∢, \end{matrix}

tehát

Y''

A X

félegyenesen van, továbbá

\begin{matrix} \frac{A Y''}{A C''} = \frac{A Y'}{A C'} = \frac{A Y}{A C} = \frac{A X}{A B} = \frac{A X}{A C''}, \end{matrix}

ennélfogva

A Y'' = A X

, amint állítottuk.
Jelöljük

B

-nek ugyanígy elforgatott, majd a zsugorítással keletkező képét

B'

-vel, ill.

B''

-vel. Ekkor

\begin{matrix} B'' X = B'' Y'' = λ \cdot B' Y' = λ \cdot B Y = λ \cdot C X, \end{matrix}

tehát

\begin{matrix} B'' X : C X = λ = A B : A C, \end{matrix}

a keresett

Y

pontnak

B''

-től és

C

-től mért távolságainak aránya egyenlő az

A

-ban összefutó oldalak arányával.
Ez a

B''

pont egyértelműen megszerkeszthető az

A

B

C

pontokból. Ismeretes másrészt, hogy azoknak a pontoknak a halmaza (mértani helye), amelyekre nézve két előírt ponttól mért távolságaik aránya állandó, kör, ha

λ \neq 1

‐ az adott pontokhoz és arányhoz tartozó ún. Apollóniosz-féle kör ‐ illetve

λ = 1

esetén a két pont közti szakasz felező merőlegese.
Második mértani helyet ad

X

-re az

A B

szakasz felező merőlegese, hiszen az előírás szerint

X A = X B

.
Tüstént látjuk, hogy

A B = A C

esetén a két mértani hely egyetlen közös pontja az

A B

oldal felezőpontja, ez viszont elfajult háromszöget eredményez. Ennélfogva csak a

λ \neq 1

esettel foglalkozunk.
A szerkesztés lépései: 1. A

B'

C'

forgatások után az

A B'

félegyenesből a

B

-n átmenő és

C' B'

-vel párhuzamos egyenessel kimetsszük

B''

-t.

2. Az Apollóniosz-körnek először a

B'' C

egyenesen levő

D^{*}

D^{* *}

pontjait szerkesztjük meg. A

D^{*} D^{* *}

szakasz átmérő, hiszen a mértani hely nyilvánvalóan szimmetrikus a

B'' C

tengelyre. Tetszőleges irányú párhuzamosokat húzunk

C

-n és

B''

-n át, felmérjük az elsőre a

C F = C A

szakaszt, a másodikra

B''

-től mindkét irányban

B A

hosszát. Ezek végpontjai

E^{*}

E^{* *}

. Így az

F E^{*}

F E^{* *}

egyenes metszi ki

D^{*}

-ot,

D^{* *}

-ot, és ,ekkor

D^{*} B'' : D^{*} C = D^{* *} B'' : D^{* *} C = B A : C A

.
Most már a

D^{*} D^{* *}

átmérőjű körből

A B

felező merőlegese metszi ki az

X

és

X_{2}

megoldásokat. Végül ezekből a rendre hozzájuk tartozó

Y

-t,

Y_{2}

-t

A

centrumú forgatva nyújtással kapjuk, szöge

B A C ∢

, aránya

1 : λ

.
A szerkesztést előkészítő elemzés (analízis) visszafordításával beláthatja az olvasó ‐ ráhagyjuk ‐, hogy a kapott

X

Y

X_{2}

Y_{2}

pontokra teljesülnek a feladat feltételei, legfőképpen a

C X = B Y

és

C X_{2} = B Y_{2}

egyenlőségek.
Annak belátását is ráhagyjuk az olvasóra, hogy

λ \neq 1

esetén mindig két megfelelő

X

Y

pontpár jön létre.
Ezzel teljesítettük feladatunkat.

Megjegyzések. 1. Feltűnhet a figyelmes olvasónak, hogy a kör éppen átmegy a

B

ponton. De tüstént beláthatja azt is, hogy ez szükségszerűség.
2. Számos dolgozat foglalkozott az

A B X

és

A C Y

háromszögek hasonlóságának olyan eseteivel is, amikor nem az ugyanannyiadik csúcspárok felelnek meg egymásnak, továbbá amikor a két betűzés körüljárási iránya ellentétes. Abból csináltak problémát, hogy kifelé vagy befelé írják rá a háromszögéket az

A B

A C

oldalakra. Ez egyrészt megérthető "hasonló példák'' alapján, másrészt éppen azt jelenti, hogy nem azt olvasták ki, hogy elsősorban pontpárt keresünk, hanem csak a mellékfeltételt.
Megemlítjük, hogy más megfeleltetésű hasonló háromszögpárral foglalkozott az F.2401. feladat (megoldása az 1983. novemberi számban, 119. old.), ott

A B E

és

C A D

voltak hasonlók (de nem szükségképpen egyenlő szárúak), és az az itteni jelölés szerint

A B X

és

C A Y

lenne.

II. megoldás. Számítás alapján megszerkesztjük az egyenlő szárú háromszögeknek az

A B

és

A C

alapon levő szögét. Legyenek a háromszög csúcsainak koordinátái

A (0,2 d)

B (2 e,0)

C (2 f,0)

, ahol

d > 0

f > 0

és

f > | e |

, ezáltal eleve

A C > A B

, kizártuk az érdektelen

A C = A B

esetet (2. ábra). Legyenek továbbá az oldalak felezőpontjai rendre

C_{1}

A_{1}

B_{1}

C B A ∢ = β

, és a forgási irányt beleértve

B A X ∢ = C A Y ∢ = φ

2. ábra

Ekkor

A_{1}

B_{1}

C_{1}

koordinátái

(e + f, 0)

;

(f, d)

, valamint

(e, d)

, és

X

abszcisszája

\begin{matrix} e + C_{1} X \cdot sin β = e + \frac{A B}{2} tg φ \cdot \frac{2 d}{A B} = e + d tg φ = e + d u, \end{matrix}

ahol rövidítésül

u = tg φ

, ezt fogjuk megszerkeszteni. Hasonlóan

X

ordinátája és

Y

koordinátái

\begin{matrix} d + e u, Y (f + d u, d + f u), \end{matrix}

így a

B Y = C X

követelményből négyzetre emeléssel, majd rendezéssel

\begin{matrix} {(f + d u - 2 e)}^{2} + {(d + f u)}^{2} = {(e + d u - 2 f)}^{2} + {(d + e u)}^{2}, \\ u^{2} + \frac{8 d}{e + f} u - 3 = 0, & (1) \end{matrix}

ugyanis

e + f > 0

.
A (

- 3

)-as állandó tagból látjuk, hogy (1)-nek két különböző valós gyöke van, ellentett előjelűek, továbbá abszolút értékre nézve a negatív gyök a nagyobb, mert

u

együtthatója pozitív.
Azt állítjuk, hogy a megfelelő

φ

szögeket megkaphatjuk a következő eljárással. Legyen az

O A_{1}

szakasz

A_{1}

-hez közelebbi negyedelő pontja

D

, mérjük föl

A_{1}

-t irány és nagyság szerint

A

-ból:

A E = A_{1} D

, messe a

D E

átmérőjű kör az

O A

egyenest

P_{1}

-ben és

P_{2}

-ben, ekkor a keresett szögek

φ_{1} = A E P_{1} > 0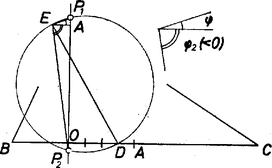

és

φ_{2} = A E P_{2} < 0

(3. ábra).

3. ábra

Igazolásul általában belátjuk a következő grafikus eljárás helyességét. Az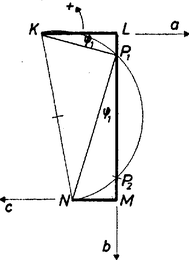

\begin{matrix} f (x) = a x^{2} + b x + c = 0 \end{matrix}

egyenlet valós gyökeit az együtthatókból képezett

K L M N

vázból kaphatjuk, ahol

K L ⊥ L M ⊥ M N

, és a

K L

L M

M N

irányított szakaszok hossza

K L = a

L M = b

M N = c

(4. ábra). Az

a

b

c

tengelyeken a pozitív irány egymás után (

- 90^{\circ}

)-kal fordul el.

4. ábra

Ekkor a

K N

átmérőjű kör által

L M

-ből kimetszett

P_{1}, P_{2}

pontokkal a gyökök

\begin{matrix} x_{1} = tg L K P_{1} ∢, x_{2} = tg L K P_{2} ∢, \end{matrix}

és a szögek irányítása az órajárással ellentétes irányú.
Legyen

P az L M

egyenes tetszőleges pontja és

L K P ∢ = φ

, továbbá messe a

P

-ben

K P

-re állított merőleges az

M N

egyenest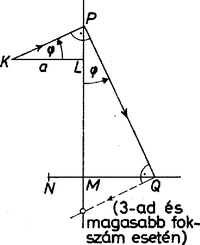

Q

-ban.

5. ábra

Ekkor nagyság és irány szerint (5. ábra)

\begin{matrix} L P = a tg φ, & P M = a tg φ + b, \\ M Q = P M tg φ, & Q N = M Q + M N, \end{matrix}

tehát

\begin{matrix} Q N = (a tg φ + b) tg φ + c = f (x), \end{matrix}

egyenletünk bal oldalának értéke a

tg φ = x

helyen.
Mármost szerkesztésünkben a Thalész-kör folytán a

P_{1}

-ben (

P_{2}

ben) állított merőleges éppen

N

-ben metszi az

M N

egyenest, így

Q N = 0

, ami igazolja állításunkat.
Ezt az eljárást föntebb (1)-nek

\begin{matrix} \frac{1}{4} u^{2} + \frac{2 d}{e + f} u - \frac{3}{4} = 0 & (1') \end{matrix}

alakjára alkalmaztuk,

K

L

M

N

megfelelője rendre

E

A

O

és

D

. Amikor a

\frac{2 d}{e + f}

együttható megfelelőjének

A O = 2 d

-t vettük,

e + f = 1

lett, majd

O D = = - 3 / 4

, végül

E A = + 1

. Ezzel igazoltuk, hogy a 3. ábra

A E P_{i} ∢ = φ_{i}

szögeire

tg φ_{i} = u_{i}, (i = 1, 2)

, és ezek valóban eleget tesznek (1)-nek.

Megjegyzések. 1. Bevezetve a

B A_{1} A ∢ = ω

jelölést, az

\begin{matrix} u^{2} + 4 u tg ω - 3 = 0 \end{matrix}

egyenletet oldottuk meg. Ebből az az érdekesség olvasható ki, hogy

u_{1}

és

u_{2}

értéke közös mindazokra az

A B^{*} C^{*}

háromszögekre, amelyekben

A

és

A_{1}

közös, továbbá

B^{*}

és

C^{*}

az eredeti

B C

egyenesnek

A_{1}

-re nézve szimmetrikus pontpárja. (Vajon mi adódik ebből

X

Y

mértani helyéül, ha

B

minden megengedett helyzetét felveszi?)
Erre a "tangenses'' értelmezésre támaszkodva egy kis túlzással mondhatjuk: a használt grafikus eljárást a mi feladatunkra találták ki.
2. A másodfokú egyenlet látott grafikus megoldását LILL-féle eljárásnak nevezik. Kiterjeszthető tetszőleges fokszámú valós együtthatós algebrai egyenlet gyökeinek közelítő keresésére, egyrészt a további együtthatóknak megfelelő törésvonalak és a

P, Q, ...

törési pontok hozzácsatolásával, másrészt azzal, hogy

Q

-ból a

P Q

-ra merőlegesen haladunk tovább.

3

-ad- és magasabb fokú egyenlet esetében azonban nincs olyan fogás a Thalész-kör helyett, amely biztosan átvisz

K

-ból

N

-be. Ilyenkor csak próbálgatni lehet

φ

(ill.

P

) változtatásával. A

K P Q ...

törött vonal újabb és újabb szerkesztése helyett egyszerűbb, gyorsabb, ha átlátszó alapra nyomtatott grafikonpapír (milliméter papír) egy darabjának megfelelő beállításával próbálkozunk.
A váz elkészítésében a

0

és negatív együtthatók megfelelő felmérése nagy gondosságot kíván.