Feladat: F.2457 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Hetyei Judit 
Füzet: 1984/október, 306 - 307. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek nevezetes tételei, Logikai feladatok, Feladat
Hivatkozás(ok):Feladatok: 1984/január: F.2457

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először belátjuk a következőt. Ha 4 pont úgy helyezkedik el a síkon, hogy 1 közülük a másik 3 által meghatározott háromszög belsejében van, akkor a 4 pontból kiválasztható két ponthármas, amelyek által meghatározott két háromszögben a legkisebb szög különböző. (Legkisebb szögről itt abban az értelemben a beszélünk, hogy a szóban forgó szögnél nincs kisebb szöge a háromszögnek.)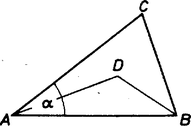
Ha ugyanis D az ABC háromszög belső pontja, és BAC∢=α az ABC háromszög legkisebb szöge (1. ábra), akkor pl. az ABD háromszög legkisebb szöge biztosan kisebb α-nál. Jelölje ε az ABD háromszög legkisebb szögét. Egyrészt ε≦BAD∢, másrészt BAD∢<BAC∢, ezért ε<α.
 
 
1. ábra
 

Mármost ha a 6 adott pont konvex burka háromszög, négyszög vagy ötszög, mindig található az előbbi tulajdonsággal rendelkező pontnégyes. Minthogy semelyik 3 pont sincs egy egyenesen, a konvex burok belsejében is található pont. Azt, hogy egy belső pont valamelyik ponthármas által meghatározott háromszögbelső pontja is egyben, biztosítja, hogy semelyik 3 pont nem esik egy egyenesre.
Ezekben az esetekben tehát a feladat állítása bizonyított.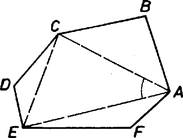
 
 
2. ábra
 

Ha a 6 megadott pont konvex burka hatszög (2. ábra), akkor válasszuk ki a hatszögnek minden második csúcsát, pl. A-t, C-t és E-t. Az ACE háromszög legkisebb szöge legyen mondjuk a CAE∢. Mivel CAD∢<CAE∢, az ACD háromszög legkisebb szöge kisebb az ACE háromszög legkisebb szögénél.
Ezzel a feladat állítását minden lehetséges esetre bebizonyítottuk.
 

Megjegyzés. 1. A fenti megoldás gondolatmenetét alkalmazva a következő erősebb állítás is belátható: Ha öt pont közül semelyik három nincs egy egyenesen, s bármely három által meghatározott háromszögben ugyanakkora a legkisebb szög, akkor az öt pont szabályos ötszöget alkot. Ebből a feladat állítása következik, hiszen hat pont közül nem alkothat bármelyik öt szabályos ötszöget.
 

2. A szabályos hatszög bármely három csúcsa és a kimaradó három csúcs egymással egybevágó háromszöget alkot. A feladat szövegéből tehát nem hagyható el a "nem feltételenül diszjunkt'' feltétel.
 

3. A szabályos nyolcszög csúcsai közül bármely három által alkotott háromszögben 22,5°-os vagy 45°-os a legkisebb szög. Nyílt kérdés azonban,  hogy kilenc pont közül kiválasztható-e mindig három olyan (nem feltétlenül diszjunkt) ponthármas, amelyek által alkotott háromszögek legkisebb szöge páronként különböző.