| Feladat: | F.2456 | Korcsoport: 18- | Nehézségi fok: - |
| Megoldó(k): | Balázsi Edina , Biró A. , Bujdosó 419 L. , Darabont T. , Diczházi Cs. , Fülöp T. , Gulyás Katalin , Hajós Zsuzsanna , Hegedűs P. , Hetyei Judit , Ilosvay Ferenc , Ispány Márton , Katona Gy. , Kerner Anna , Krajnyák Kornélia , Ladányi L. , Limbek Cs. , Link P. , Pfeil T. , Pintér A. , Ribényi Á. , Róka G. , Sárközy G. , Selyem I. , Simon Gy. , Somogyi 196 A. , Stipsicz A. , Szabó 529 G. , Uhlmann E. , Zabó T. , Zuba Andrea | ||
| Füzet: | 1984/október, 304 - 306. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkgeometriai számítások trigonometria nélkül négyszögekben, Szögfüggvények, síkgeometriai számítások, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1984/január: F.2456 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. a) Jelöljük a deltoid csúcsait sorra betűvel úgy, hogy és legyen, az átlók hosszát -vel, metszéspontjukat -mel. Feltehetjük, hogy adatainkra teljesül. 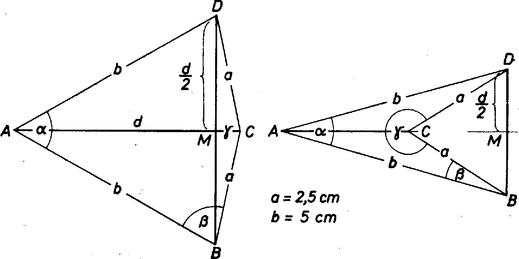 Eleve gondolunk konvex és konkáv megoldás lehetőségére. Az és derékszögű háromszögek alapján , azaz Valós értéket kapunk, ha a diszkriminánsra Ez esetén mindenesetre teljesül: , és felső korlátját az
Ha (3)-ban , akkor geometriailag csak a megoldás használható (négyzet), mert a megoldás elfajult négyszöget jelent. Akkor is csak 1 deltoidot kapunk, ha , ekkor (2) gyökei egyenlők. Általában ahol , és kifejezésében a négyzetgyök -szerese szerepel. b) Valós, nem elfajult megoldás esetén a -ra és -ra a cosinustétel alapján, mindkét -értékkel és ezekből a csúcsnál levő szög A eset tulajdonképpen szintén elfajult deltoid. Előre látható, hogy szükségképpen ez áll be, ha , ekkor (1) mindkét oldala 0, és . Meg lehet mutatni, hogy a eset úgy vágja ketté a (3) intervallum belsejét, hogy esetén konvex négyszöget eredményez, konkávot; ha pedig Megjegyzés. Bizonyára több megoldó észrevette, hogy feladatunk a múlt tanévi Gy. 2045. gyakorlat számító megoldása; ott az oldalakból szerkesztenünk kellett a deltoidot, tudva, hogy . (Lásd a megoldást az 1983. decemberi számban, 206. old.) Az ottani megoldás a átlónak a merőleges helyzetbe való forgatásán alapul. Természetesen lép be a diszkusszióba a szám: , ami nálunk kerülő úton, szerencsés észrevétellel érkezett be. 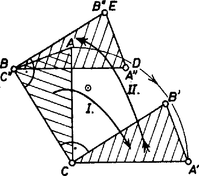 E meglátás alapján a gépies Pitagorasz-tétel helyett más, közvetett megoldások is kínálkoznak. Például a felhasználásával: Lényegében ugyanígy használható segédszögnek a is. Ott végül is a feltételhez jutottunk, az elfajult eseteket nem emeltük ki. |