Kezdőlap


Feladat:	F.2454	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1984/november, 365 - 368. oldal		PDF \| MathML
Témakör(ök):	Térfogat, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1984/január: F.2454

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha $m$ és $n$ adott pozitív egészek, $x$ adott szakasz, akkor hasonló háromszögek segítségével $\frac{m}{n} \cdot x$ könnyen szerkeszthető. Például két, közös $A$ pontból induló félegyenes egyikére felmérjük az $A B = m x$ szakaszt, a másikra egy tetszőleges $A C_{0}$ szakasz $n$ -szeresét, $A C$ -t. A $C_{0}$ ponton keresztül a $C B$ egyenessel húzott párhuzamos az $A B$ szakaszból éppen az $A B_{0} = \frac{m}{n} \cdot x$ hosszú szakaszt metszi ki (1. ábra).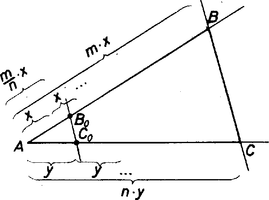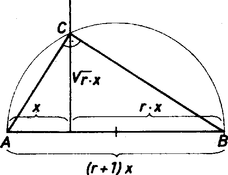

1. ábra

2. ábra

Legyen most

r

tetszőleges pozitív racionális szám.

\sqrt[]{r} \cdot x

egy olyan derékszögű háromszögnek az átfogóhoz tartozó magassága, amelynek átfogóját a magasság éppen

r x

és

x

hosszú szakaszokra osztja (2. ábra). A

\sqrt[]{r} \cdot x

ennek alapján például a következőképpen szerkeszthető: az

(r + 1) x

hosszúságú szakasz fölé Thalesz-kört rajzolunk, majd az átmérő végpontjától

x

távolságra merőleges félegyenest állítunk. A félegyenes a kört éppen

\sqrt[]{r} x

távolságra metszi. A feladat olyan

y

és

z

hosszúságú szakaszok szerkesztését kívánja, amelyekre

y^{3} + z^{3} = x^{3}

. Legyen

\begin{matrix} y + z = t \cdot x . & (1) \end{matrix}

Ezzel a jelöléssel az

x^{3} = y^{3} + z^{3} = (y + z) (y^{2} - y z + z^{2})

a következőképpen írható:

\begin{matrix} y^{2} - y z + z^{2} = \frac{x^{2}}{t} . & (2) \end{matrix}

Emeljük (1)-et négyzetre, vonjuk ki belőle (2)-t, osszunk

3

-mal, majd vonjunk gyököt:

\begin{matrix} \sqrt[]{y z} = x \sqrt[]{\frac{t^{2}}{3} - \frac{1}{3 t}} . & (3) \end{matrix}

Nyilvánvaló, hogy (3)-ból és (1)-ből (2) következik, (1) és (2)-ből pedig

x^{3} = = y^{3} + z^{3}

. Elég tehát olyan

y

és

z

hosszúságú szakaszokat szerkeszteni, amelyekre (1) és (3) fennáll. Ha

t

pozitív racionális szám és

\begin{matrix} \frac{t^{2}}{3} - \frac{1}{3 t} > 0, azaz t > 1, \end{matrix}

akkor a megoldás elején mondottak szerint

t \cdot x

és

x \cdot \sqrt[]{t^{2} / 3 - 1 / (3 t)}

hosszúságú szakaszt tudunk szerkeszteni. Az

y + z = t x

átfogójú,

\sqrt[]{y z}

magasságú

A B C

derékszögű háromszög

C

csúcsának vetülete az

A B

átfogót éppen a keresett

y

és

z

hosszúságú szakaszokra osztja.
Ha tehát

t > 1

, akkor a következő szerkesztés megfelelő

y

és

z

szakaszokat szolgáltat: megszerkesztjük az

A B = t x

hosszúságú szakaszt és fölé a Thalész-kört. Az

A B

egyenestől

x \sqrt[]{t^{2} / 3 - 1 / (3 t)}

távolságra futó

e

egyenest a megoldás elején mondottak alapján tudunk szerkeszteni. Ha

e

metszi a Thalész-kört, akkor a metszéspontok megfelelnek

C

-nek. Ezek

A B

-re eső merőleges vetületei az átfogót olyan

A D

és

D B

szakaszokra osztják, melyek hosszára (1) és (3) fennáll, és éppen ilyen szakaszokat kerestünk (3. ábra).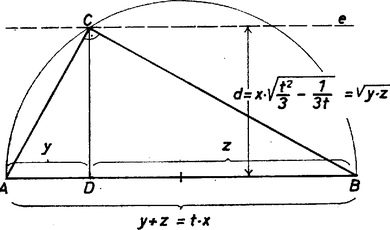

3. ábra

Azt kell még megállapítanunk, választható-e

t

úgy, hogy

e

messe a Thalész-kört. Ez pontosan azt jelenti, hogy az

x \sqrt[]{t^{2} / 3 - 1 / (3 t)}

távolság nem haladhatja meg a

t x

átmérő felét, azaz fenn kell állnia a következő egyenlőtlenségnek:

\begin{matrix} \sqrt[]{\frac{t^{2}}{3} - \frac{1}{3 t}} \leq \frac{t}{2}, vagyis t^{3} \leq 4. \end{matrix}

Szerkesztésünk tehát tetszőleges

1 < t \sqrt[3]{4}

racionális számból elvégezve megoldáshoz vezet, így pl.

t = 3 / 2

esetén is: ekkor

A B = 3 x / 2

és

C D = \sqrt[]{19} x / 6

II. megoldás. Az előző megoldás elején mondottak szerint tetszőleges pozitív

a

b

racionális számokra az

(a + \sqrt[]{b}) x

és

(a - \sqrt[]{b}) x

szakaszokat meg tudjuk szerkeszteni, feltéve hogy

\begin{matrix} a > \sqrt[]{b}, azaz a^{2} > b > 0 és a > 0. & (4) \end{matrix}

Keressük most

y

-t és

z

-t ilyen alakban. (Megjegyezzük, hogy az előző megoldás is ilyen alakú

y

és

z

-hez vezet.) Ekkor

\begin{matrix} y^{3} + z^{3} = ({(a + \sqrt[]{b})}^{3} + {(a - \sqrt[]{b})}^{3}) x^{3} = (2 a^{3} + 6 a b) x^{3} . & (5) \end{matrix}

a

és

b

tehát pontosan akkor felel meg, ha

2 a^{3} + 6 a b = 1

, vagyis ha

\begin{matrix} b = \frac{1 - 2 a^{3}}{6 a} . & (6) \end{matrix}

(4) és (6) összevetéséből

a^{2} > (1 - 2 a^{3}) / (6 a) > 0

, azaz

\frac{1}{2} < a < \frac{1}{\sqrt[3]{2}}

adódik. Válasszuk tehát az

a

racionális számot

1 / 2

és

1 / \sqrt[3]{2}

között tetszőlegesen. Ekkor

b = \frac{1 - 2 a^{3}}{6 a} > 0

b

racionális és persze

a - \sqrt[]{b} > 0

. Így az

y = (a + \sqrt[]{b}) x

és a

z = (a - \sqrt[]{b}) x

hosszúságú szakaszokat meg tudjuk szerkeszteni,

y

és

z

-re (5) és (6) alapján

y^{3} + z^{3} = x^{3}

teljesül, a feladatot megoldottuk.

a

választható például

2 / 3

-nak.

III. megoldás. Az

y

-t és a

z

-t ezúttal

y = x sin α

z = x sin β

alakban keressük, ahol

α

β

szerkeszthető szögek. Az

x^{3} = y^{3} + z^{3}

feltétel ekkor

sin 3 α = = 3 sin α - 4 sin^{3} α

alapján így írható:

\begin{matrix} 1 = sin^{3} α + sin^{3} β = \frac{3 sin α - sin 3 α + 3 sin β - sin 3 β}{4} = \frac{3}{2} sin \frac{α + β}{2} cos \frac{α - β}{2} - \\ - \frac{1}{2} sin \frac{3 α + 3 β}{2} cos \frac{3 α - 3 β}{2} = 1. \end{matrix}

Vegyük észre, hogy ha

α + β = 120^{\circ}

, akkor

sin \frac{3 α + 3 β}{2} = 0

és

sin \frac{α + β}{2} = \frac{\sqrt[]{3}}{2}

. A fenti egyenlőség tehát így alakul:

\begin{matrix} \frac{3 \sqrt[]{3}}{4} cos \frac{α - β}{2} = 1, \end{matrix}

azaz

\begin{matrix} cos \frac{α - β}{2} = \frac{4}{3 \sqrt[]{3}} . & (7) \end{matrix}

4

egység befogójú és

3 \sqrt[]{3} > 4

átfogójú derékszögű háromszögnek a

4

hosszúságú befogója mellett fekvő szöge éppen a

\frac{α - β}{2}

, ami kisebb

60^{\circ}

-nál. Másrészt

\frac{α + β}{2} = 60^{\circ}

a feltevésünk szerint, így

α

-t,

β

-t meg tudjuk szerkeszteni, és ebből a pozitív

y = x sin α

és

z = x sin β

is szerkeszthető. A fenti számolást (7)-ből kiindulva visszafelé is elvégezhetjük, s ahhoz jutunk, hogy a szerkesztett szögekre

sin^{3} α + sin^{3} β = 1

, vagyis

y^{3} + z^{3} = x^{3}

, ahogy a feladat kívánta.

Megjegyzés. Többen észrevették, hogy a feladatnak köze van az ún. déloszi problémához, mely azt a feladatot tűzte a görögök elé, hogy szerkesszenek olyan kockát, amelynek térfogata kétszerese egy adott kocka térfogatának. Sok szellemes kísérlet után csak a 19. század végén sikerült bizonyítani, hogy körzővel és vonalzóval ilyen kocka éle nem szerkeszthető. A mi feladatunk nyelvén ez azt jelenti, hogy

y = z

feltevéssel a feladatot nem lehet megoldani. Az I. megoldás bizonyos értelemben az összes szóba jövő

(y \neq z)

megoldást megadja: ha

t

olyan szám, amelyre

t x

szerkeszthető és

1 < t < \sqrt[3]{4}

, akkor (1) és (3) megoldható és a megoldás szerkeszthető. Ezt még könnyű bizonyítani, de azt már nem könnyű megmondani, milyen

t

számokra szerkeszthető a

t x

hosszúság. (Erről bővebbet lásd a KöMal 14. kötet (1957) 4‐5. számaiban a 97‐107. és 129‐134. oldalakon, Surányi János: A szögharmadolás kérdéséről c. cikkében.)
Megjegyezzük még, hogy egyes tudósok szerint a déloszi probléma felvetése a déloszi jósdánál működő görög papok (talán szándékos) félreértése volt. Vallási szokás volt ugyanis bizonyos járványok idején a (kocka alakú) oltárt olyan kockára bővíteni, amelynek alapterülete az eredeti kocka alapterületének kétszerese.