Kezdőlap


Feladat:	F.2431	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1984/január, 12 - 14. oldal		PDF \| MathML
Témakör(ök):	Ceva-tétel, Kombinatorikai leszámolási problémák, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 1983/szeptember: F.2431

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög csúcsait $A$ , $B$ , $C$ betűvel, az $A$ -tól $B$ felé haladva átlépett osztópontokat sorra $C_{1}, C_{2}, ..., C_{11}$ -gyel, és $B$ -től $C$ -ig, majd tovább $A$ -ig hasonlóan $A_{1}, A_{2}, ..., A_{11}$ , $B_{1}, B_{2}, ..., B_{11}$ -gyel. Az $A A_{6}$ , $B B_{6}$ , $C C_{6}$ összekötő szakaszok a háromszög szimmetriatengelyei, közös pontjuk a háromszög $O$ középpontja.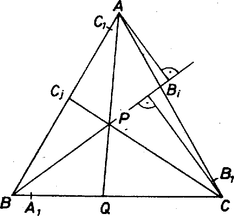

A tengelyeken levő minden metszésponton hasonlóan

2

másik összekötés megy át, pl.

A A_{6}

és

B B_{i}

közös pontján

C C_{12 - i}

(i = 1,2, ...,11)

, hiszen

B_{i}

és

C_{12 - i}

nyilván tükrös pontpár az

A A_{6}

tengelyre nézve. Ezek a metszéspontok tehát akkor is létrejönnének, ha az

A A_{6}

B B_{6}

C C_{6}

tengelyeket nem rajzolnánk be vagy pedig ha töröljük őket.
Valóban, az

i = 6

-hoz tartozó összekötéseket tovább ott nem levőknek tekintjük, csak

O

címén majd

1

-et hozzáadunk a megállapítandó létszámhoz. Így a háromszög mindegyik csúcsából

10

összekötés indul ki ‐ nevezzük ezeket röviden ferdéknek ‐ , és mindegyik metszi a további csúcsokból induló

10 + 10

ferde összekötést, mert pl. a

B B_{i}

szakasz elválasztja

A

-t minden

A_{i}

-től és

C

-t minden

C_{i}

-től. E pillanatban tehát

30 \cdot 20 / 2 = 300

metszéspontra gondolunk, hacsak nincs olyan pont, amelyen három ferde megy át.
Megmutatjuk, hogy nincs további hármas metszéspont. Jelöljük

B B_{i}

és

C C_{j}

metszéspontját

P

-vel ‐ ami belső pontja a háromszögnek ‐ , az

A P

egyenesnek a

B C

oldalszakaszon levő pontját

Q

-val, ekkor állításunk szerint

Q

nem tartozik az

A_{K}

osztópontok közé. Természetesen

i \neq 6

és

j \neq 6

, sőt

j \neq 12 - i

, különben

Q = A_{6}

következnék be.
Tekintsük a

B P A

és

B P C

háromszögek területének arányát. Közös alapjuk

B P

, tehát az arányt megadja az erre merőleges magasságok aránya, ezt pedig az

A B_{i}

és

C B_{i}

, oldalaik aránya. Hosszúságegységnek

A C_{1}

-et választva

\begin{matrix} \frac{t_{B P A}}{t_{B P C}} = \frac{A B_{i}}{B_{i} C} = \frac{12 - i}{i} (i \neq 6) . \end{matrix}

Ugyanígy

\begin{matrix} \frac{t_{C P B}}{t_{C P A}} = \frac{B C_{j}}{C_{j} A} = \frac{12 - j}{j} (j \neq 6, j \neq 12 - i), \end{matrix}

és e kettő szorzatából, egyszerűsítés útján

\begin{matrix} \frac{t_{A P B}}{t_{A P C}} = \frac{A B_{i} \cdot B C_{j}}{B_{i} C \cdot C_{j} A} = \frac{(12 - i) (12 - j)}{i j} . \end{matrix}

A bal oldalt önállóan is kifejezhetjük az előbbiek mintájára:

\begin{matrix} \frac{t_{A P B}}{t_{A P C}} = \frac{t_{A Q B}}{t_{A Q C}} = \frac{B Q}{Q C}, \end{matrix}

ugyanis a második arányban szereplő háromszögek rendre úgy jöttek létre az elsőben szereplőkből, hogy a közös

A P

alapot

A Q / A P

arányban növeltük, a harmadik csúcsokat pedig változatlanul hagytuk, tehát a magasságok nem változtak meg. Ezek alapján

\begin{matrix} \frac{A B_{i} \cdot B C_{j}}{B_{i} C \cdot C_{j} A} = \frac{B Q}{Q C}, \end{matrix}

másképpen

\begin{matrix} \frac{A B_{i} \cdot B C_{j} \cdot C Q}{B_{i} C \cdot C_{j} B \cdot Q B} = 1, & (1) \\ \frac{12 - i}{i} \cdot \frac{12 - j}{j} \cdot \frac{12 - q}{q} = 1, & (2) \end{matrix}

ahol

q = B Q

, amelyre

0 < q < 12

és nyilván

q \neq 6

. Azt akarjuk belátni, hogy

q

nem egész szám.
Föltesszük, hogy

q

mégis egész, és belátjuk, hogy így (2) nem teljesülhet. Mindenesetre az előbbiekhez hasonlóan

12 - q \neq i