Feladat: F.2402 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Hetyei Gábor 
Füzet: 1983/szeptember, 14 - 15. oldal  PDF  |  MathML 
Témakör(ök): Parabola egyenlete, Lefedések, Feladat
Hivatkozás(ok):Feladatok: 1983/január: F.2402

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vizsgáljuk meg, hogy mi lehet a közös része egy egyenesnek és egy parabola tartománynak. Vegyük föl a koordináta‐rendszert úgy, hogy a parabola egyenlete y=x2 legyen, ekkor az egyenes egyenlete vagy y=ax+b, vagy x=c alakú (a,b,c tetszőleges). Az x=c egyenletű egyenesek párhuzamosak a parabola tengelyével, ezek a parabola tartományt félegyenesben metszik.
Az y=ax+b egyenes és a parabola tartomány közös részének koordinátái kielégítik az x2≦ax+b és y=ax+b feltételeket. Látható, hogy ez egy szakaszra teljesül, vagy nincs közös rész.
Tegyük föl most, hogy adott a síkon véges sok parabola tartomány, és válasszunk egy olyan egyenest, mely nem párhuzamos egyik parabola tengelyével sem. Ebből az egyenesből a parabolák legfeljebb véges sok szakaszt fednek le, tehát még ezt az egyenest sem fedik le teljesen a parabola tartományok, ennélfogva az egész síkot sem.

 

II. megoldás. Két segédtételt használunk fel,
1. segédtétel. Bármely parabola tartomány lefedhető tetszőlegesen kicsi pozitív φ szögű tartománnyal.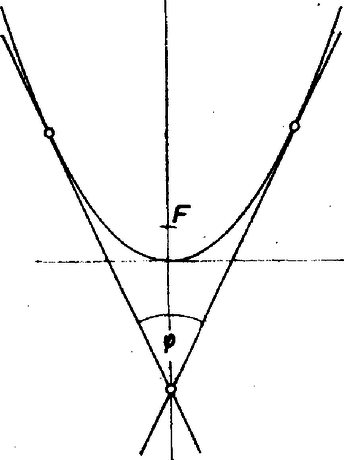
Válasszuk úgy a derékszögű koordinátarendszer tengelyeit, hogy a parabola egyenlete y=x2/2p legyen, ahol p a fókusz és a vezéregyenes távolsága. Az (x0,x02/2p) ponthoz húzott érintő meredeksége megegyezik az y=x2/2p függvény deriváltjának az x0 helyen vett értékével, azaz x0/p-vel. Ha |x0| nő, akkor a meredekség abszolút értéke is minden határon túl nő. Így az érintőnek az y tengellyel bezárt szöge tetszőlegesen kicsire csökkenthető. A (-x0,x02/2p) és (x0,x02/2p) pontokhoz húzott érintők által meghatározott szögtartomány lefedi a parabola tartományt. A két határoló félegyenes 2-szer akkora szöget zár be egymással, mint amekkora szöget az y tengely és az (x0,x02/2p) ponthoz húzott érintő közrezár, és ez a szög is tetszőlegesen kicsire csökkenthető.
Vegyünk fel a síkon n db parabola tartományt, s fedjük le e tartományok mindegyikét egy, közös φ szögű tartománnyal, ahol 0<φ<π/2n. Ezzel többet fedünk le a síkból, mint a parabola tartományok.
Jelöljük a szögtartományok csúcsait P1,P2,...,Pn-nel és r-rel a P1Pi; távolságok legnagyobbikát, i=2,3,...,n. Mivel véges sok (n-1) db szakasz maximálisát vettük, így r is véges. A P1=O középpontú, r sugarú körlap tartalmazza P1,P2,...,Pn mindegyikét. Látni fogjuk, hogy a szögtartományok már ezt a körlapot sem fedik le.
2. segédtétel. Ha egy hegyesszög‐tartomány P csúcsa egy r sugarú kör határán vagy a belsejében van, akkor a szögtartomány legfeljebb 2r2⋅φ területű részét fedi le a körnek, ahol φ a szögtartomány mértéke radiánban.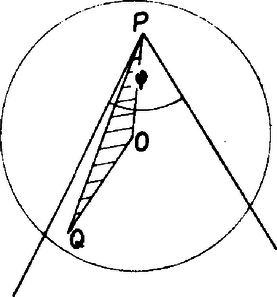
 

 
Legyen ugyanis Q a szögtartomány és a körlap tetszőleges közös pontja. Mivel P és Q az O középpontú, r sugarú körlap pontjai, így OP≦r és OQ≦r. A háromszög ‐ egyenlőtlenség szerint PQ≦OP+OQ≦2r, tehát Q benne van a P középpontú 2r sugarú, φ szögű körcikkben. Ez a körcikk tartalmazza tehát a szögtartomány és a kör közös részét, s a közös rész területe emiatt legfeljebb akkora, mint a körcikk területe, ami T=2r2φ.
Ezek szerint a P1,P2,...,Pn csúcsú szögtartományok bármelyike legföljebb T=2r2φ területű részt fed le a P1=O középpontú r sugarú körből. Az n db szögtartomány legfeljebb n⋅T területet fed le a körlapból, az pedig φ megválasztása folytán kisebb, mint r2π, a kör területe, vagyis a szögtartományok együtt valóban nem fedik le a kört. Így nem fedik le teljesen a síkot sem.
 
 Hetyei Gábor (Pécs, Leöwey K. Gimn., IV. o. t.)