Feladat: F.2401 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Alexy N. ,  Böröczky L. ,  Danyi P. ,  Erdős 228 L. ,  Fóris Z. ,  Megyesi G. ,  Nyikes P. ,  Pásztor L. ,  Reichardt J. ,  Réz A. ,  Szemők Á. ,  Takács T. ,  Tóth G. ,  Törőcsik J. 
Füzet: 1983/november, 119 - 120. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Síkgeometriai számítások trigonometria nélkül háromszögekben, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):Feladatok: 1983/január: F.2401

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek az ABE háromszög oldalai rendre a, b és e, ekkor az ABE és CAD háromszögek hasonlósága alapján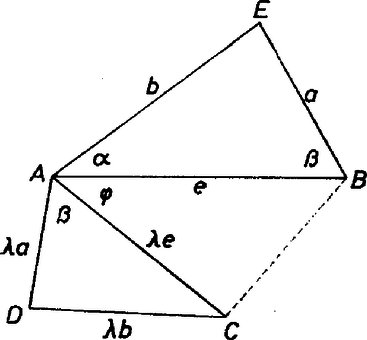

AD=λa,DC=λb,AC=λe
valamilyen pozitív λ-val. Az AB és CA oldalak nagyságviszonyát λ dönti el: ha λ<1, akkor az AB oldal a nagyobb; ha λ=1, akkor AB=CA; végül ha λ>1, akkor a CA oldal a nagyobb. Így ahhoz, hogy a kérdésre választ adhassunk, elegendő megvizsgálni, λ milyen értékei egyeztethetők össze a BD=CE feltétellel.
 
 

Jelöljük a BAC szöget φ-vel, ekkor a cosinustétel alapján
BD2=e2+(λa)2-2λaecos(β+φ),CE2=b2+(λe)2-2λbecos(α+φ).


Innen BD=CE akkor és csak akkor áll, ha (mindjárt átrendezve és az addíciós képleteket felhasználva)
λ2(a2-e2)-2λcosφ(aecosβ-becosα)+(e2-b2)=(1)=-2λesinφ(asinβ-bsinα).


A jobb oldalon az ABE háromszögre vonatkozó sinustétel alapján 0 áll. A cosinustételből könnyen adódó
aecosβ-becosα=a2-b2
összefüggést (1)-be írva adódik, hogy BD=CE akkor és csak akkor áll fenn, ha
λ2(a2-e2)-2λcosφ(a2-b2)+(e2-b2)=0.(2)

Innen azonnal leolvasható, hogy az a=b=c esetben ‐ azaz ha az ABE, és ezzel együtt a CAD háromszög is szabályos ‐ (2) azonosan teljesül, vagyis a BD=CE egyenlőség minden λ, és φ mellett fennáll. Így általában az AB és CA oldalak nagyságviszonyáról ‐ egyedül a BD=CE alapján ‐ semmit sem mondhatunk.
 

Ha a=b≠e, azaz ABE olyan egyenlő szárú nem‐szabályos háromszög, melynek alapja AB, akkor (2) szerint BD=CE akkor és csak akkor, ha λ2=1. Ha tehát ABE ilyen háromszög, akkor BD=CE esetén az AB és AC oldal egyforma hosszúságú.
 

Végül ha a≠b, akkor (2)-t a következő alakra hozhatjuk:
2cosφ=λa2-e2a2-b2+1λ⋅e2-b2a2-b2.(3)
Ez teljesül, ha λ=1 és φ=60∘, ekkor (3) mindkét oldalának értéke 1. Mivel (3) jobb oldala λ>0-ra λ-nak folytonos függvénye, található olyan (a-tól, b-től és e-től függő) ε>0, hogy 1-ε<λ<1+ε esetén (3) jobb oldalának értéke a (2cos70∘, 2cos50∘) intervallumba esik. Következésképp minden, az (1-ε, 1+ε) intervallumba eső λ-hoz található olyan 50∘<φ<70∘, mellyel (3) teljesül, azaz amikor BD=CE fennáll. Tehát BD=CE mellett a λ<1, λ=1 és a λ>1 esetek mindegyike felléphet: az AB és AC oldalak nagyságviszonyáról semmit nem mondhatunk.
Összefoglalva: ha az ABE háromszögben AE=EB≠AB, akkor BD=CE csak úgy állhat fenn, ha az AB és CA oldalak egyenlő hosszúak. Minden más esetben BD=CE fennállhat úgy is, ha AB<CA, úgy is, ha AB=CA, és úgy is, ha AB>CA.