Kezdőlap


Feladat:	F.2383	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1983/április, 150 - 151. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1982/október: F.2383

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az adott háromszög $A B C$ , amelyben $A B$ az átfogó, oldalai szokásosan $a$ , $b$ , $c$ . Minden beírt négyzetből két csúcsnak rajta kell lennie a háromszög valamelyik oldalán. Ha ezeket a $C A$ befogón keressük, akkor az egyik $C$ lesz, különben nem lenne négyzetcsúcs a $C B$ -n, pedig $A B$ -n ekkor csak egy csúcs lehet. Jelöljük ezt a beírt négyzetet $C D E F$ -fel, $D$ van a $C A$ -n, ennélfogva 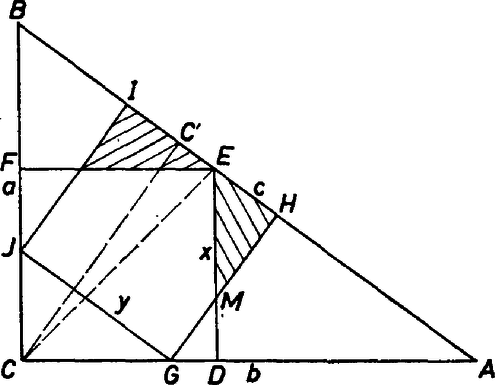$F$ a $C B$ -n.

A négyzet ilyen beírásában a

C E

átló felezi az

A C B

derékszöget, ezért

\begin{matrix} B E : E A = C B : C A = a : b \end{matrix}

és

\begin{matrix} B E : (B E + E A) = B E : c = a : (a + b), \end{matrix}

innen

B E = \frac{a c}{a + b}

.
Így a

B E F

és

B A C

háromszögek hasonlóságából a négyzet oldala

\begin{matrix} F E = \frac{b}{c} B E = \frac{a b}{a + b} \end{matrix}

Ha az

A B

átfogón kívánunk két négyzetcsúcsot ‐ legyenek ezek

H

és

I

‐, ezeket a

C C'

magasság szétválasztja, hiszen a

H I

-vel párhuzamos

G J

négyzetoldal végpontjai nem lehetnek ugyanazon a befogón. Legyenek

H

és

G

C C'

-nek

A

-t tartalmazó oldalán, és legyen

I J = I H = y

.
A három részre darabolt átfogó szélső darabjai, hasonló háromszögek felhasználásával

\begin{matrix} B I = \frac{a}{b} y, A H = \frac{b}{a} y, \end{matrix}

és hozzájuk véve

I H

-t, a háromszög

A B

átfogóját kapjuk, amiből

\begin{matrix} y = \frac{c}{\frac{a}{b} + 1 + \frac{b}{a}} = \frac{a b c}{a^{2} + a b + b^{2}} . \end{matrix}

G

csúcs az

a / b

aránynak minden értéke mellett a

C D

szakaszon van, mert

\begin{matrix} C G = \frac{b}{c} J G = \frac{a b^{2}}{a^{2} + a b + b^{2}} = C D \cdot \frac{a b + b^{2}}{a^{2} + a b + b^{2}} < C D, \end{matrix}

hasonlóan

J

C F

szakasz pontja. Másrészt

I

mindig a

B E

szakaszon és

H

A E

-n van, mert

\begin{matrix} \frac{B I}{B E} = \frac{a (a + b)}{a^{2} + a b + b^{2}} < 1 és \frac{A H}{A E} = \frac{b (a + b)}{a^{2} + a b + b^{2}} < 1. \end{matrix}

Ezek szerint a két négyzet közös része az

E L J G M

ötszög, ahol

L

E F

I J

szakaszpár,

M

pedig az

E D, H G

pár közös pontja: második négyzetünkből el kell hagynunk az

E I L

és az

E H M

háromszöget.
Ezek befogói az előbbi részeredmények felhasználásával

\begin{matrix} E I = B E - B I = \frac{a b^{2} c}{(a + b) (a^{2} + a b + b^{2})} = \frac{b}{a + b} \cdot y, \\ I L = \frac{a}{b} E I = \frac{a}{a + b} \cdot y, \end{matrix}

továbbá hasonló számítás eredményeként

H E = I L

és

H M = I E

.
Ezek alapján a keresett terület

\begin{matrix} y^{2} - E I \cdot I L = y^{2} (1 - \frac{a b}{{(a + b)}^{2}}) = \frac{a^{2} + a b + b^{2}}{{(a + b)}^{2}} \cdot y^{2} = \frac{a^{2} b^{2} (a^{2} + b^{2})}{{(a + b)}^{2} (a^{2} + a b + b^{2})} . \end{matrix}

Megjegyzés. Ha a befogók helyett az átfogót és az egyik hegyesszöget tekintjük adottnak, akkor a két négyzet közös részének területe

\begin{matrix} \frac{c^{2}}{2} \cdot \frac{sin^{2} 2 α}{(1 + sin 2 α) (2 + sin 2 α)} ≦ \frac{c^{2}}{12} . \end{matrix}

A felső korlátot

α = 45^{\circ}

mellett éri el a terület, és ekkor

1 / 3

része az eredeti háromszög területének.