Kezdőlap


Feladat:	F.2373	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ákosfai Z. , Alberti G. , Almássy T. , Ambrus L. , Balázs Z. , Beke S. , Bobák Emese , Csillag P. , Danyi P. , Drávucz Katalin , Erdős 228 L. , Fóris Z. , Frei Zs. , Fritz P. , Kapovits Á. , Kardon B. , Kedves M. , Kovács 123 L. , Lenkó Cs. , Mohay T. , Nagy Zs. , Nyikes P. , Papp 193 G. , Peták T. , Polgár L. , Raffai Zs. , Simák Gy. , Spanyiel Ilona , Szekeres G. , Szemők Á. , Tranta Beáta , Törőcsik J. , Vindics I. , Wágner P. A. , Weisz F. , Zieger B.
Füzet:	1983/február, 63 - 66. oldal		PDF \| MathML
Témakör(ök):	Parabola egyenlete, Feladat, Síkgeometriai bizonyítások, Egyenesek egyenlete, Paraméteres egyenletek
Hivatkozás(ok):	Feladatok: 1982/május: F.2373

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A feladatot koordináta-geometriai módszerrel oldjuk meg. A koordináta-rendszer kezdőpontja legyen a parabola tengelypontja, az $y$ -tengely a parabola szimmetriatengelye. "Felfelé nyitott'' parabolát vizsgálunk, ennek egyenlete :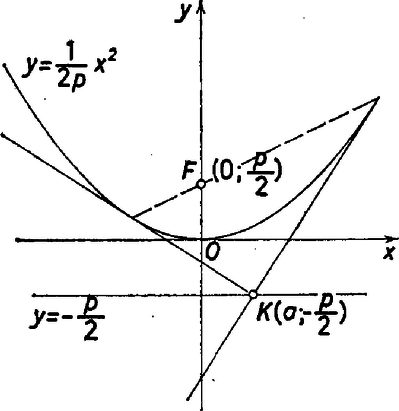

\begin{matrix} y = \frac{1}{2 p} x^{2}, \end{matrix}

ahol

p > 0

, a parabola paramétere. A parabola fókusza az

F (0; \frac{p}{2})

pont, vezéregyenese az

y = - \frac{p}{2}

egyenletű egyenes (1.ábra).

1. ábra

Egy, a parabola síkjában fekvő egyenest akkor tekintünk a parabola érintőjének, ha a parabolával egyetlen közös pontja van, és nem párhuzamos a parabola tengelyével. A vizsgált parabola érintői nem lehetnek tehát párhuzamosak az

y

-tengellyel, ezért az érintők egyenlete

y = m x + b

alakban írható.
Legyen a vezéregyenes egy tetszőleges, de rögzített pontja

K (a; - \frac{p}{2})

. A

K

pontra illeszkedő érintők egyenlete ilyen alakú lesz:

\begin{matrix} y = m (x - a) - \frac{p}{2}, \end{matrix}

ahol

m

-et kell meghatároznunk.
Az érintőnek a parabolával egy közös pontja van, ezért az

\begin{matrix} \frac{1}{2 p} x^{2} = m (x - a) - \frac{p}{2} \end{matrix}

vagyis az

\begin{matrix} x^{2} - 2 p m x + 2 p m a + p^{2} = 0 \end{matrix}

másodfokú egyenlet diszkriminánsának zérusnak kell lennie :

\begin{matrix} 4 p^{2} m^{2} - 4 (2 p m a + p^{2}) = 0. \end{matrix}

Ennek alapján a két érintő meredeksége :

\begin{matrix} m_{1} = \frac{1}{p} (a - \sqrt[]{a^{2} + p^{2}}) és m_{2} = \frac{1}{p} (a + \sqrt[]{a^{2} + p^{2}}) . \end{matrix}

P_{1}, P_{2}

érintési pontok

x

koordinátáját az egyenlet kétszeres gyöke,

x = p m

adja,

y

koordinátáját pedig

y = \frac{1}{2 p} x^{2}

\begin{matrix} P_{1} [a - \sqrt[]{a^{2} + p^{2}}; \frac{1}{2 p} (2 a^{2} + p^{2} - \sqrt[]{a^{2} + p^{2}})], \end{matrix}

\begin{matrix} P_{2} [a + \sqrt[]{a^{2} + p^{2}}; \frac{1}{2 p} (2 a^{2} + p^{2} + 2 a \sqrt[]{a^{2} + p^{2}})] . \end{matrix}

P_{1} P_{2}

egyenes egyenlete az

(x_{2} - x_{1}) (y - y_{1}) = (y_{2} - y_{1}) (x - x_{1})

séma szerint

\begin{matrix} 2 \sqrt[]{a^{2} + p^{2}} [y - \frac{1}{2 p} (2 a^{2} + p^{2} - 2 a \sqrt[]{a^{2} + p^{2}})] = \frac{2 a}{p} \sqrt[]{a^{2} + p^{2}} [x - (a - \sqrt[]{a^{2} + p^{2}})] . \end{matrix}

x = 0

esetén, tekintve, hogy

\sqrt[]{a^{2} + p^{2}} \neq 0

\begin{matrix} y = \frac{1}{2 p} (2 a^{2} + p^{2} - 2 a \sqrt[]{a^{2} + p^{2}}) - \frac{a}{p} (a - \sqrt[]{a^{2} + p^{2}}) = \frac{p}{2} . \end{matrix}

Ezzel igazoltuk, hogy a fókuszpont illeszkedik a P1P2 egyenesre.

Bobák Emese (Jászárokszállás, Solymosi I. Gimn., III. o.t.)

II. megoldás. Bebizonyítjuk, hogy a parabola egy tetszőleges

P

pontjából a fókuszhoz húzott vezérsugár és a

P

pontból a vezéregyenesre bocsátott merőleges szögét felező egyenes érinti a parabolát.
Legyen

P

a parabolának egy tetszőleges pontja.

P

-ből a

v

vezéregyenesre bocsátott merőleges talppontját jelölje

G

, a parabola fókuszpontját

F

(2. ábr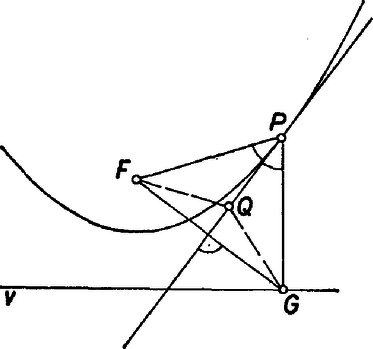a).

2. ábra

Belátjuk, hogy az

P F G ∢

szögfelezőjének semelyik

P

-től különböző

Q

pontja nem lehet a parabolán.
Mivel az

F P G ∢

sohasem

0

, az

F P G ∢

szögfelezője nem párhuzamos a parabola tengelyéve], és ennek megfelelően nem merőleges a vezéregyenesre. A szögfelezőn ezért

P

az egyetlen pont, amelynek merőleges vetülete a vezéregyenesen

G

.
Az

F P G ∢

szögfelezője egyúttal az

F G

szakasz felező merőlegese is, hiszen a parabola definíciója szerint

P F = P G

. Így a szögfelező tetszőleges

Q

pontja ugyanakkora távolságra van

F

-tőI, mint

G

-től, de a szögfelezőn csak a

P

pont van ugyanakkora távolságra

G

-től, mint a vezéregyenestől.
Ezek után a feladat megoldása már könnyen adódik. Tekintsük a parabolának egy, a vezéregyenest

K

-ban metsző érintőjét (3. ábra).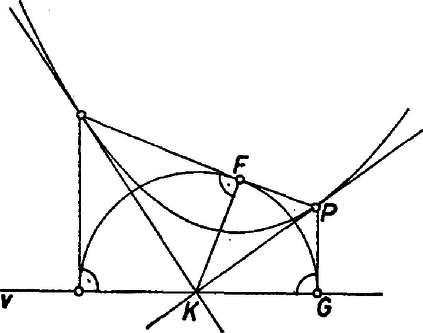

3. ábra

Mivel

K

az érintőn van,

K G = K F

. A

P F K

háromszög ezért egybevágó a

P G K

háromszöggel. Ebből következik, hogy

P F K ∢ = P G K ∢ = 90^{\circ}

, vagyis a vezéregyenes

K

pontjából a parabolához húzott érintő

P

érintési pontját

F

-fel összekötő egyenes merőleges a

K F

egyenesre. Mivel ez igaz a

K

pontra illeszkedő másik érintőre is, az érintési pontok és a fókuszpont valóban egy egyenesen vannak.

Tranta Beáta (Miskolc, Földes F. Gimn., IV. o. t.)

Megjegyzések. 1. Néhány dolgozat a

(0; 1)

pontot tekintette az

y = x^{2}

parabola fókuszának, egyúttal az

y = - 1

egyenest használta fel mint vezéregyenest. Látszólag bebizonyították az állítást egy ál-fókuszra és ál-vezéregyenesre. Közelében jártak a következő tételnek.
Jelöljön

e

egy a vezéregyenessel párhuzamos, rögzített egyenest,

E

ennek egy tetszőleges pontját,

T_{1}

és

T_{2}

E

-ből húzott érintők érintési pontját, végül

G

T_{1} T_{2}

egyenesnek a tengelyen levő pontját. Ekkor

G

állandó pont, éspedig rajta van

e

-nek a csúcsérintőre való tükörképén (4. ábra).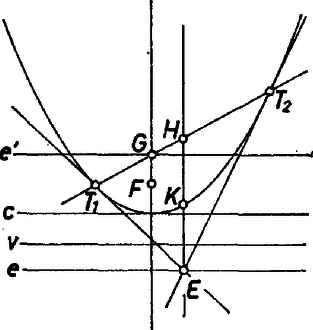

4. ábra

Legyen a parabola

y = x^{2}

, ekkor érintőjének iránytényezője az

(x_{1}, x_{1}^{2})

pontban

2 x_{1}

, az érintő egyenlete

y - x_{1}^{2} = 2 x_{1} (x - x_{1})

. Legyen

x_{2} \neq x_{1}

, az

(x_{2}, x_{2}^{2})

pontbeli,

y = 2 x_{2} x - x_{2}^{2}

egyenletű érintő, ez az előbbit az

x = (x_{1} + x_{2}) / 2

abszcisszán metszi. Ezt tekintjük E-nek, ordinátája

x_{1} x_{2}

.
Végül a

T_{1} T_{2}

egyenes egyenlete

(y - x_{1}^{2}) (x_{2} - x_{1}) = (x_{2}^{2} - x_{1}^{2}) (x - x_{1})

, ennek pedig az

x = 0

abszcisszájú pontjához az

y = - x_{1} x_{2}

ordináta tartozik.
Ha

e

azonos a vezéregyenessel, akkor

G

azonos a fókusszal.
2. Kapcsolatba hozhatják az érdeklődők az előbbieket a következőkkel. Jelölje a

T_{1} T_{2}

húr felezőpontját

H

, az

E H

szakasz felezőpontját

K

. Ekkor

K

rajta van a parabolán és

E H

párhuzamos a tengellyel.