Kezdőlap


Feladat:	F.2372	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Alberti G. , Balázs Z. , Fekete Zs. , Szemők Á. , Tranta Beáta , Törőcsik J. , Zieger B.
Füzet:	1983/január, 9 - 11. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1982/május: F.2372

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. I. rész. 1. A csuklókat $A$ , $B$ , $C$ , $D$ betűvel jelöljük. Az $A B = 23$ , $B C = 20$ , $C D = 15$ , $D A = 10$ megválasztással sikerült egy kör kerületére hozni a csuklókat úgy, hogy akármelyik szakasz egyeneséhez képest a nem rajta fekvő csuklók ugyanazon a parton vannak. (Az $A B C D$ négyszög konvex.) Ezt a megfelelő sugár kiszámításával igazoljuk.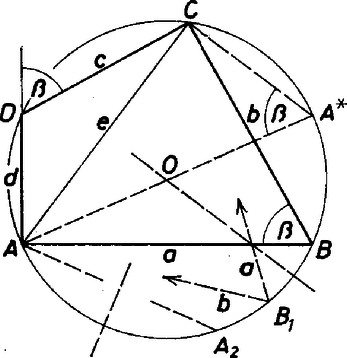

1. ábra

Felhasználjuk még az

A C = e

és

A B C ∢ = β

méreteket (1. ábra). Ekkor

C D A ∢ = 180^{\circ} - β

, és a cosinustétel szerint, a szakaszok hosszát rendre

a

b

c

d

-vel jelölve

\begin{matrix} e^{2} = a^{2} + b^{2} - 2 a b cos β = c^{2} + d^{2} + 2 c d cos β, \end{matrix}

hiszen

cos (180^{\circ} - β) = - cos β

. Innen

\begin{matrix} cos β = \frac{(a^{2} + b^{2}) - (c^{2} + d^{2})}{2 (a b + c d)} = \frac{604}{1220} \end{matrix}

révén

β = 60^{\circ}

, 325, továbbá

e^{2} = 57 770 / 122

e = 21, 761

, végül az

A A^{*} C

derékszögű háromszögből ‐ ahol

A A^{*}

átmérő és

A A^{*} C ∢ = β

‐

\begin{matrix} A A^{*} = \frac{e}{sin β} = 25, 045, r_{1} = 12, 523 egység . \end{matrix}

Kiemeljük, hogy az eredmény egyértelműen adódott, a négy szakasz hossza és föltételezett sorrendje egyértelműen meghatározta a belőlük adódó húrnégyszög körülírt körének sugarát.
2. A

cos β

és

e^{2}

kifejezések nem változnak meg

a

és

b

fölcserélésével úgyszintén a

c

d

cserével sem. Eszerint ugyanez a

β

e

és

r_{1}

érték adódik a következő sorrendekből is (az eredeti

a

b

c

d

mellé):

b

a

c

d

;

a

d

b

c

; a két újabb sorrend azonban csak a körüljárás irányában különbözik egymástól.
3. Leolvasható a felcserélhetőség az 1. ábráról is, ahol

B_{1}

B

csukló tükörképe az

A C

átló felező merőlegesére. Így ugyanis

A B_{1} = C B = b

és

B_{1} C =

= B A = a

, továbbá

B_{1}

is a körön van, tehát az ugyanazon körbe írt, ugyancsak konvex

A B_{1} C D

húrnégyszög is megvalósítható az adott szakaszok más sorrendjével.
4. A kiindulásban a

c

szakasz volt. az

a

-val szemben (nem csatlakozóan), az

A B_{1} C D

-ben pedig a

d

szakasz. Szemben levővé tehetjük

a

-val a

b

szakaszt is úgy, hogy pl.

A

-t a

B D

átló felező merőlegesére tükrözzük

A_{2}

-be, mert

A_{2}

is a körön van, és

A_{2} D = A B = a

, valamint

A_{2} B = A D = d

. Most a

D A_{2} B C

négyszögben

a

d

b

c

a szakaszok sorrendje.
Ezek szerint ha a szakaszok konvex négyszöget zárnak közre, akkor bármilyen sorrendjük mellett ugyanakkora sugarat kapunk arra a körre, amely mind a négy csuklót tartalmazza, hiszen az

a

szakasz és a vele szemben fekvő

c

d

, ill.

b

esetével végigvettünk a további két szakasz szembenállására is minden lehetőséget.
A sorrend fölcserélhetősége szemléletesen azt jelenti, hogy az

A O B

B O C

C O D

és

D O A

körcikkeket tetszés szerinti sorrendben összerakhatjuk teljes körré.
II. rész. Próbáljunk most hurkolt

K M N P

húrnégyszöget összeállítani az egymástól különböző

k

m

n

p

szakaszokból, ebben a sorrendben, a 2. ábra szerint.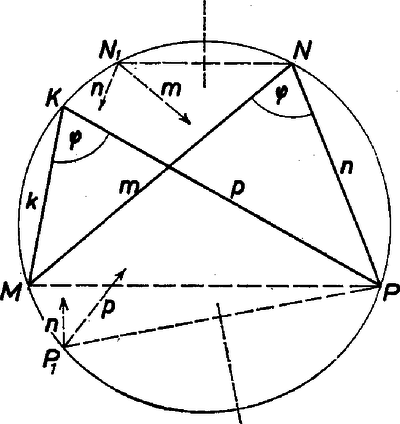

2. ábra

Tegyük fel, hogy sikerült ez. Látni ebből, hogy így az

N

-nek az

M P

húr felező merőlegesére való

N_{1}

tükörképét felhasználva, a

K M N_{1} P

is hurkolt négyszög és az is megfelelő, de az

m

szakasz kerül

k

-val szembe. (Nem lehet, hogy

N_{1}

azonos legyen

K

-val, mert abból

n = k

következnék Továbbá

P

-nek a

K N

felező merőlegesére való

P_{1}

tükörképével

K M N P_{1}

is megfelelő, és ebben

p

áll

k

-val szemben. Ha tehát létezik hurkolt megoldás, akkor minden lehetséges sorrendben kapcsolhatók a szakaszok. Más szóval: a négyszög létezése nem a sorrenden múlik.
Jelöljük a talált kör sugarát

r_{2}

-vel és legyen még

M P = q

M K P ∢ =

= M N P ∢ = φ

. Az előbbi számításhoz hasonlóan

\begin{matrix} cos φ = \frac{(k^{2} + p^{2}) - (m^{2} + n^{2})}{2 (k p - m n)}, \end{matrix}

hacsak

k p \neq m n

, és ha a jobb oldal kisebb, mint 1.
Mivel adataink egész számok, és köztük a 23 prímszám, ezért a nevező nem tűnik el. Abból is látni ezt, hogy három olyan adatunk van, amely 5-nek első hatványával osztható.
Vegyük a

k = 23

m = 20

n = 15

p = 10

szereposztást, ebből

cos φ =

= - 1 / 35

φ = 91^{\circ} 637'

q^{2} = 4495 / 7

és

r_{2} = 12, 675

.
Szemléletesen azt jelenti a sorrendnek a hurkolt négyszögben való megváltoztatása, hogy a csuklók közti körívekhez tartozó körcikkek "egymás után'' rakásában alkalmas két cikk után visszafordulunk. A kiszámított

r_{2}

-vel a szakaszokhoz tartozó középponti szögek

130,^{\circ} 26; 104,^{\circ} 17; 72,^{\circ} 56

és

46,^{\circ} 47

, a két szélső összege egyenlő a belsők összegével. Visszafordulás esetén azonban a

360^{\circ}

-ra kiegészítő

229,^{\circ} 74

, szöggel számoljon az érdeklődő.
Feladatunkat tehát két sugárméret elégíti ki, mindegyik meghatározza a csuklós négyszög konvex, ill. hurkolt jellegét, a szakaszok sorrendjét azonban nem.

Megjegyzések. 1. Természetes, ha a számadatokat csak elindításnak tekintjük, és legalább numerikusan megnézünk néhány más helyzetet.
Csak akkor lehet szó megoldásról, ha szakaszaink legnagyobbika kisebb, mint a többiek összege. Ez azonban hurkolt megoldáshoz nem elegendő, a 3. ábrán egy ilyesféle példát vázolunk:

k = 100

m = 1

n = 60

p = 40

, és ezekből

cos φ = 1, 015

lenne. Ekkor nincsen megfelelő kör.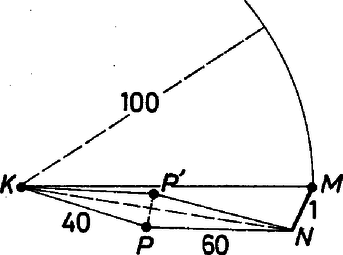

3. ábra

2. Nem szükségképpeni ‐ mint a feladatban adódott ‐, hogy

r_{2} > r_{1}

legyen. Lehet

r_{2} = r_{1}

is, ha

k^{2} + p^{2} = m^{2} + n^{2}

, vagyis a szakaszok négyzetösszege két egyenlő részre tagolható, az egyik átló éppen átmérő.
Más példa: a 20, 20,

x

x