Kezdőlap


Feladat:	F.2362	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1982/december, 197 - 198. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletrendszerek, Vektorok, Feladat
Hivatkozás(ok):	Feladatok: 1982/április: F.2362

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vezessük be az $u = \frac{x + y}{2}$ és a $v = \frac{x - y}{2}$ jelöléseket. Ezekkel $x = u + v, y = u - v$ , és egyenletrendszerünk a következőképpen alakul:

\begin{matrix} 2 cos u cos v = 2 cos^{2} u - 1, & (1) \\ 2 sin u cos v = 2 sin u cos u . & (2) \end{matrix}

(1) alapján

cos u \neq cos v

, hiszen

2 cos^{2} u \neq 2 cos^{2} u - 1

, így (2) pontosan akkor teljesül, ha

sin u = 0

, azaz

\begin{matrix} u = k π \end{matrix}

valamilyen

k

egész számmal. Ekkor

cos u = {(- 1)}^{k}

, és (1)-ből

cos v = {(- 1)}^{k} / 2

, azaz

\begin{matrix} v = \pm \frac{π}{3} + k π + 2 l π, \end{matrix}

ahol

l

egész szám. Az (1) és (2) egyenleteket ezek és csak ezek az

u

v

számok elégítik ki, így az eredeti egyenletrendszer megoldásai

\begin{matrix} x = u + v = \pm \frac{π}{3} + 2 (k + l) π, y = u - v = \mp \frac{π}{3} + 2 l π, \end{matrix}

ahol

k

és

l

tetszőleges egészek.

II. megoldás. Jelöljük az első koordináta-tengely pozitív irányával

x

, illetve

y

szöget bezáró egységvektort

a

-val, illetve

b

-vel, az

x + y

szöget bezáró egységvektort pedig

c

-vel. Jelöléseink mellett a feladat egyenletrendszere ekvivalens a

\begin{matrix} c = a+b \end{matrix}

(3)

egyenlettel. Jelöljük továbbá az origót

O

-val, az

O

-ból induló

a

b

c

vektorok végpontját pedig

A

-val,

B

-vel,

C

-vel.
Mivel

a, b

egységvektorok, a (3) egyenlet azt jelenti, hogy a következő három eset valamelyike következik be :
1.

a

és

b

egyirányúak, ekkor

c

a kétszeresük;
2.

a

és

b

ellentétes irányúak, ekkor

c

null-vektor;
3. az

O A C B

négyszög paralelogramma.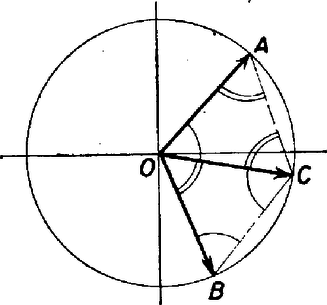

Mivel másfelől

c

is egységvektor, csak a harmadik eset jöhet szóba. Ekkor

A C ∥ O B

B C ∥ O A

miatt az

O

-nál levő szögek

C

-nél is megjelennek, és

O A = O C = O B

miatt átmásolhatóak

A

-ba,

B

-be. Ámde ekkor csak

60^{\circ}

-osak lehetnek, és emiatt

\begin{matrix} x = \pm 60^{\circ} + n \cdot 360^{\circ}, \\ y = \mp 60^{\circ} + m \cdot 360^{\circ}, \end{matrix}

ahol

n

m

tetszőleges egészek.