Feladat:	F.2361	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1982/november, 131. oldal		PDF  |  MathML
Témakör(ök):	Függvényvizsgálat, Téglatest, Térfogat, Feladat
Hivatkozás(ok):	Feladatok: 1982/március: F.2361

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.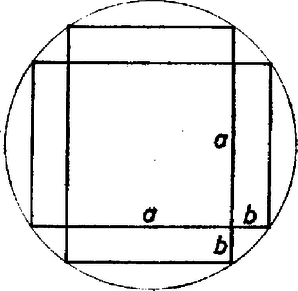 Jelöljük a kör átmérőjét $D$-vel, a doboz űrtartalmát $V$-vel, Pitagorasz tétele szerint $\begin{array}{c}{\displaystyle {\left(a+2b\right)}^2+a^2=D^2\mathrm{,}}\end{array}$ tehát ez a mennyiség független az $a$, $b$ méretek $\begin{array}{c}{\displaystyle x=\frac{a}{b}}\end{array}$ arányától. Ezt az arányt úgy kell meghatároznunk, hogy $\begin{array}{c}{\displaystyle V=a^{2}b}\end{array}$ maximális legyen, vagy ami ugyanezt jelenti, az $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{D^2}{V^{2/3}}+\frac{{\left(a+2b\right)}^2+a^2}{{\left(a^{2}b\right)}^{2/3}}=\frac{{\left(x+2\right)}^2+x^2}{x^{4/3}}}\end{array}$ függvény értéke minimális legyen. Annak érdekében, hogy kényelmesebben tudjunk deriválni, vezessük be az $\begin{array}{c}{\displaystyle x=y^3}\end{array}$ változót. Mivel a feladat geometriai jelentése szerint $x>0$, az új változó a réginek monoton függvénye, így alkalmazása a szélső érték keresését nem zavarja meg. Így a $\begin{array}{c}{\displaystyle g\left(y\right)=\frac{{\left(y^3+2\right)}^2+y^6}{y^4}=2y^2+\frac{4}{y}+\frac{4}{y^4}}\end{array}$ függvény maximumát kell meghatároznunk az $y>0$ feltétel mellett. A függvény deriváltja $\begin{array}{c}{\displaystyle g\text{'}\left(y\right)=\frac{4}{y^2}\left(y^3-1-\frac{4}{y^3}\right)}\end{array}$ az $y$ monoton növő függvénye, tehát csak egyetlen helyen lehet $0$-val egyenlő. Itt maga a függvény fogyóból növőbe vált át, tehát minimuma van. Mivel a derivált értéke akkor $0$, ha $\begin{array}{c}{\displaystyle x-\frac{4}{x}=1}\end{array}$ ez a feltétel határozza meg az $x$ arány keresett értékét. A $x^2-x-4=0$ másodfokú egyenlet pozitív gyöke $x=\frac{1+\sqrt[]{17}}{2}$, tehát ez az $a/b$ hányados értéke akkor, amikor a doboz űrtartalma maximális.