Kezdőlap


Feladat:	F.2360	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Alberti G. , Böröczky K. , Danyi P. , Fritz P. , Hetyei G. , Kovács 254 Ildikó , Kovács123 L. , Lengyel Zs. , Magyar Á. , Megyesi Gábor , Mohay T. , Szuhai Erika , Tóth 360 G. , Törőcsik J. , Weisz F.
Füzet:	1982/november, 127 - 130. oldal		PDF \| MathML
Témakör(ök):	Beírt kör, Súlypont, Kör egyenlete, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1982/március: F.2360

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Azt várjuk, hogy a súlypontnak a beírt körre való illeszkedése alapján valamilyen összefüggés írható fel a háromszög alkalmas alkotó részei között. Előkészítésül ilyet keresünk; a szokásos jelöléseket használjuk.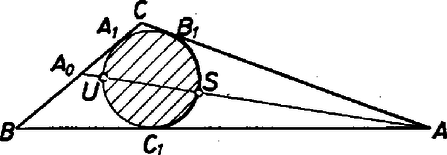
A beírt körnek az $A B$ , $B C$ , $C A$ oldalon levő $C_{1}$ , $A_{1}$ , $B_{1}$ érintési pontjai a kört három ívre osztják, válasszuk úgy a betűzést, hogy az $S$ súlypont az $A_{1}$ -et nem tartalmazó $B_{1} C_{1}$ íven legyen. Más szóval ─ a kört átlátszatlannak tekintve ‐ $S$ az $A$ csúcsból látható, $B$ -ből és $C$ -ből nem látható. Jelöljük a kör és az $A A_{0}$ súlyvonal második közös pontját $U$ -val, ez tehát az $S A_{0}$ szakaszon van. Legyen továbbá $A C ≦ A B$ , így $A_{1} C ≦ A_{0} C$ , tehát $A_{1}$ az $A_{0} C$ szakaszon van, esetleg $A_{0}$ -ban.

Kétszer alkalmazzuk a szelő‐érintő tételt, előbb az

A

, majd az

A_{0}

-ból kifutó félegyeneseken levő szakaszokra:

\begin{matrix} A S \cdot A U = A B_{1}^{2}, A_{0} S \cdot A_{0} U = A_{0} A_{1}^{2} . \end{matrix}

(Felírhatjuk ezeket az

A S B_{1}

és

A B_{1} U

, illetve

A_{0} U A_{1}

és

A_{0} A_{1} S

háromszögpárok hasonlósága alapján is.)
Ismeretes, hogy

A B_{1} = (b + c - a) / 2

, hasonlóan

A_{0} A_{1} = A_{0} C - C A_{1} = a / 2 - (a + b - c) / 2 = (c - b) / 2 (≧ 0)

. Legyen még

A_{0} U = u

és

A_{0} A = d

, ekkor

A_{0} S = d / 3

és

A S = 2 d / 3

, hiszen

S

harmadolja

A A_{0}

-t ; másrészt az

A C D B

paralelogramma oldalai és átlói közti összefüggés alapján

\begin{matrix} 4 d^{2} = 2 b^{2} + 2 c^{2} - a^{2}, \end{matrix}

(ez is ismert összefüggés). Mindezekkel

\begin{matrix} A B_{1}^{2} + 2 A_{0} A_{1}^{2} = \frac{2 d}{3} (d - u) + \frac{2 d}{3} u = \frac{2 d^{2}}{3}, \end{matrix}

\begin{matrix} \frac{{(b + c - a)}^{2}}{4} + \frac{{(c - b)}^{2}}{2} = \frac{2 b^{2} + 2 c^{2} - a^{2}}{6}, \end{matrix}

végül

\begin{matrix} 5 (a^{2} + b^{2} + c^{2}) = 6 (a b + a c + b c) . \end{matrix}

(1)

Ezzel összefüggést kaptunk mindazon háromszögek oldalai között, amelyekben a beírt kör áthalad

S

-en, tekintet nélkül jelöléseink kezdeti megválasztására, hiszen a megkülönböztetett szerepű

a

oldal itt egyenrangúnak bizonyult

b

-vel és

c

-vel.
Az

a = 2 r sin α

stb. összefüggések alapján (

r

a körülírt kör sugara) a kérdéses tulajdonságú háromszögekben nyilvánvalóan ez is teljesül:

\begin{matrix} 5 (sin^{2} α + sin^{2} β + sin^{2} γ) = 6 (sin α sin β + sin α sin γ + sin β sin γ) . \end{matrix}

(2)

2. Legyen most már

γ = 120^{\circ}

, tehát

sin γ = \sqrt[]{3} / 2

és

α + β = 60^{\circ}

. Behelyettesítéssel és átrendezéssel

\begin{matrix} 5 {(sin α + sin β)}^{2} - 16 sin α sin β + \frac{15}{4} - 3 \sqrt[]{3} (sin α + sin β) = 0. \end{matrix}

A következő átalakításokkal az

x = cos \frac{α - β}{2}

ismeretlenre kapunk egyenletet:

\begin{matrix} sin α + sin β = 2 sin \frac{α + β}{2} cos \frac{α - β}{2} = 2 cos \frac{γ}{2} cos \frac{α - β}{2} = cos \frac{α - β}{2}, \end{matrix}

\begin{matrix} 2 sin α sin β = cos (α - β) - cos (α + β) = (2 cos^{2} \frac{α - β}{2} - 1) - \frac{1}{2}, \end{matrix}

végül

\begin{matrix} - 11 x^{2} - 3 \sqrt[]{3} x + \frac{63}{4} = 0. \end{matrix}

Diszkriminánsa pozitív:

720 = {(12 \sqrt[]{5})}^{2}

, gyökei valósak és ellentett előjelűek, feladatunkban csak a pozitív gyök értelmezhető:

\begin{matrix} x = \frac{12 \sqrt[]{5} - 3 \sqrt[]{3}}{22}, \end{matrix}

amiből

α ≦ β

figyelembevételével

\begin{matrix} \frac{α - β}{2} = - 10^{\circ},4275. \end{matrix}

Ezt

\frac{α + β}{2} = 30^{\circ}

-hoz hozzáadva, ill. belőle levonva:

\begin{matrix} α = 19^{\circ},5725 (= 19^{\circ} 34'), \end{matrix}

\begin{matrix} β = 40^{\circ},4275 (= 40^{\circ} 26'), \end{matrix}

a feladat kérdésére megadtuk a választ.

Megjegyzések. 1. Többen észrevették, hogy az

a

b

c

oldalakra megállapított (1) összefüggés megtalálható lapunk egy régebbi pályázatának eredménybeszámolójában K. M. L. 34 (1967) 205─212. oldal.

2.Több megoldás hivatkozott a következő tételre:

\begin{matrix} O S^{2} = ϱ^{2} - \frac{s^{2}}{3} + \frac{2}{9} (a^{2} + b^{2} + c^{2}), \end{matrix}

ahol

O

a beírt kör középpontja és

ϱ

a sugara. (Lásd pl. Szikszai József: Háromszöggel kapcsolatos feladatok koordinátageometriai megoldása, Középisk. Szakköri Füzetek, Tankönyvkiadó, Bp., 1977. 39. oldal.) Esetünkben

O S = ϱ

, tehát

3 s^{2} = 2 (a^{2} + b^{2} + c^{2})

, ebből is kiadódnék a fönti (1), de annak kialakítása nélkül is rátérhetünk a szögek számítására.

3. A felhasznált összefüggések szokatlansága nem kínált számításos módot az eredmény ellenőrzésére. Számpéldában azonban mindig rendelkezésre áll az eredmény mérethű megrajzolása, a jelen esetben hozzáértve a kört és az

S

pontot is. Ez az eljárás ─ a rajz kis pontatlanságai ellenére ─ kiáltóan megmutathatta volna, hogy a több dolgozatban is szereplő

11^{\circ},5

és

48^{\circ},5

eredmény hibás; ezekkel

O S

közel

2,5 ϱ

-val egyenlő.

II. megoldás. A koordináta-geometria módszereivel először a háromszögnek a

γ = 120^{\circ}

-os szögét bezáró

a

és

b

oldalait számítjuk ki, hosszegységnek választva a beírt

k

kör

ϱ

sugarát. Legyen

k

középpontja az origó, a

C

csúcs az tengely negatív felén,

A

a tengely alatt, így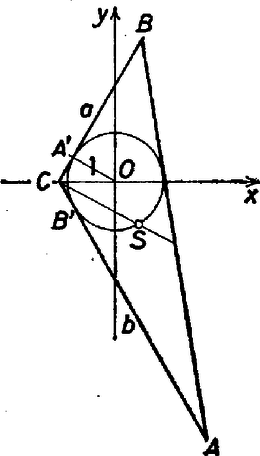

B

fölötte.

C O

felezi a

γ

szöget, tehát a

C B

oldalegyenes irányszöge

60^{\circ}

C A

-é

- 60^{\circ}

és a csúcsok, majd ezekből az

S

súlypont koordínátái:

\begin{matrix} A (- \frac{2}{\sqrt[]{3}} + \frac{b}{2}, - \frac{b \sqrt[]{3}}{2}), B (\frac{- 2}{\sqrt[]{3}} + \frac{a}{2}, \frac{a \sqrt[]{3}}{2}), \end{matrix}

\begin{matrix} C (- \frac{2}{\sqrt[]{3}}, 0), S (- \frac{2}{\sqrt[]{3}} + \frac{a + b}{6}, \frac{(a - b) \sqrt[]{3}}{6}) . \end{matrix}

S

koordinátái kielégítik a beírt kör ‐ az egységkör ‐ egyenletét:

\begin{matrix} {(- \frac{2}{\sqrt[]{3}} + \frac{a + b}{6})}^{2} + \frac{3 {(a - b)}^{2}}{36} = 1, \end{matrix}

alkalmasan átrendezve

\begin{matrix} {(a + b)}^{2} - 2 \sqrt[]{3} (a + b) - 3 a b + 3 = 0. \end{matrix}

(3)

C

-ből a körhöz húzott érintőszakaszok hossza egyfelől

C A' = 1 / \sqrt[]{3}

, másfelől az ismert összefüggés szerint

(a + b - c) / 2

, egyenlőségükből

c = (a + b) - 2 / \sqrt[]{3}

, és a cosinustételnek

c

-re való alkalmazásával

\begin{matrix} {(a + b - \frac{2}{\sqrt[]{3}})}^{2} = a^{2} + b^{2} + a b, \end{matrix}

azaz

\begin{matrix} 3 a b - 4 \sqrt[]{3} (a + b) + 4 = 0. \end{matrix}

(4)

Ezt (3)-mal egybekapcsolva egyenletrendszert kapunk az

a

és

b

oldalak összegére és szorzatára mint ismeretlenekre. Kiküszöböljük a szorzatukat:

\begin{matrix} {(a + b)}^{2} - 6 \sqrt[]{3} (a + b) + 7 = 0, \end{matrix}

\begin{matrix} a + b = 3 \sqrt[]{3} \pm 2 \sqrt[]{5} (= 9,668, ill. 0,724) . \end{matrix}

Innen csak a nagyobb gyököt használhatjuk, hiszen

a + b > 2 \cdot C A' = 2 / \sqrt[]{3} > 1

.
Most már (4) alapján

\begin{matrix} a b = \frac{32 + 8 \sqrt[]{15}}{3}, (= 20,9939) \end{matrix}

ennélfogva

a

és

b

a következő másodfokú egyenlet gyökei:

\begin{matrix} u^{2} - (3 \sqrt[]{3} + 2 \sqrt[]{5}) u + \frac{32 + 8 \sqrt[]{15}}{3} = 0. \end{matrix}

Legyen

a ≦ b

, ekkor

\begin{matrix} a, b = \frac{3 \sqrt[]{3}}{2} + \sqrt[]{5} \mp \sqrt[]{\frac{13 + 4 \sqrt[]{15}}{12}} = {\begin{matrix} 3,293, \\ 6,375. \end{matrix} \end{matrix}

Végezetül az

O A B'

, ill.

O B A'

derékszögű háromszögből

\begin{matrix} ctg \frac{α}{2} = \frac{A B'}{O B'} = b - C B', ctg \frac{β}{2} = a - C A', \end{matrix}

\begin{matrix} α = 19^{\circ},57, β = 40^{\circ},43 \end{matrix}

(amiből

α + β + γ = 180^{\circ}

). Ezzel befejeztük a megoldást.

Szuhai Erika (Miskolc, Kossuth Gimn., IV. o. t.)
Megyesi Gábor (Szeged, Ságvári E. Gyak. Gimn., I. o. t.)

Megjegyzés. Több beküldő hasonló lépésekkel

a

-ra és

b

-re szimmetrikus (más néven reciprok) egyenletre jutott, és azt ‐ szokásosan ‐ az

x + \frac{1}{x} = y

új ismeretlenre áttérve oldotta meg, két szakaszban, az ismert módon.
A föntiekben sikerült megkerülnünk ezt, mi is felhasítottuk egyenletünket két másodfokúra, és az

a + b < 1

megoldásokat eleve kizártuk.