Feladat: F.2353 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Ákosfai Z. ,  Alberti G. ,  Breiner Z. ,  Böröczky K. ,  Csörgő T. ,  Danyi P. ,  Engländer J. ,  Erdős L. ,  Hajas Csilla ,  Holbok I. ,  Ittzés A. ,  Károlyi Gy. ,  Kovács P. ,  Lenkó Cs. ,  Megyesi G. ,  Mikó Teréz ,  Papp G. ,  Somlói J. ,  Szabó E. ,  Szakszon P. ,  Szöllősi G. ,  Tóth G. ,  Tranta Beáta ,  Weisz F. 
Füzet: 1982/november, 119 - 121. oldal  PDF  |  MathML 
Témakör(ök): Paralelogrammák, Párhuzamos szelők tételének megfordítása, Síkgeometriai számítások trigonometria nélkül négyszögekben, Vektorok felbontása összetevőkre, Feladat
Hivatkozás(ok):Feladatok: 1982/február: F.2353

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Az E, F pontot egyelőre a BC, ill. CD oldalszakasz belső pontjának tekintjük. Így a DE egyenes nem párhuzamos AB-vel ‐ jelöljük közös pontjukat M-mel ‐, másrészt G az AB oldal belső pontja, hiszen centrális tükörképe F-nek a paralelogramma középpontjára; végül H az eddigiek mindegyikétől különböző pont (1. ábra).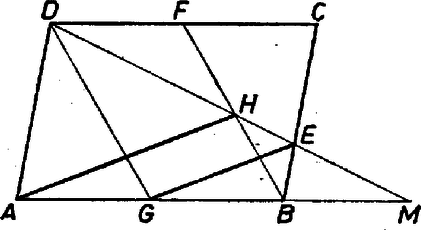

 

1. ábra
 


Az MA, MD egyeneseket kétféleképpen is átmetszettük 2‐2 párhuzamos egyenessel. Egyrészt az AD, BC oldalpárral, emiatt
EMBM=DMAM,
azaz
AM⋅EM=DM⋅BM;
másrészt a BF, DG szelőpárral, emiatt hasonlóan
GM⋅HM=DM⋅BM.

A jobb oldalak egyenlősége alapján
AM⋅EM=GM⋅HM,  azaz  AMGM=HMEM,
ez pedig a párhuzamos szelők tételének megfordítása alapján azt jelenti, hogy AH és GE párhuzamos egyenesek. A feladat állítását ezzel bebizonyítottuk.
2. Ha akár E, akár F az illető oldalszakasz valamelyikének végpontjába tolódik, vagy ha mindkettő ilyen különleges helyzetet vesz fel, akkor H is egybeesik valamelyik előbbi ponttal (B, C, D, E, F valamelyikével) vagy pedig határozatlan és az állítás semmitmondóvá válik.
3. Ha viszont E vagy F az illető oldal valamelyik meghosszabbításán van úgy, hogy H is létrejön ─ vagyis DE és BF nem párhuzamosak ─, akkor az állítás lényegében ugyanígy bizonyítható.
 

II. megoldás. 1. Jelöljük az AB→ vektort rövidebben a-val, AD→-t b-vel. A sík minden vektorát kifejezhetjük ezekkel ‐ ti. ha végpontjait pontjainkból elő lehet állítani szerkesztéssel vagy alkalmas megválasztással. E-t és F-et azzal a 0 és 1 közti λ, ill. κ számmal választjuk a paralelogramma megfelelő oldalán, hogy EC→=λb, ill. FC→=κa legyen, ekkor AG→=FC→ és GB→=(1-κ)a, továbbá BE→=(1-λ)b, és GE→=GB→+BE→=(1-κ)a+(1-λ)b.
Kifejezzük AH→-t. BF→=BC→+CF→=b-κa, és mivel H a BF-en keletkezik, van olyan α1 szám, amelyre BH→=α1 BF→=α1b-κα1a, ebből tehát AH→=AB→+BH→=(1-κα1)a+α1b.
Hasonlóan DE→=a-αb, DH→=α2DE→ és AH→=AD→+DH→=α2a+(1-λα2)b, ahol α2 alkalmas szám. Következő lépésünk éppen α1 és α2 kiszámítása lesz.
AH→ kétféle előállításának eredménye ‐ H jelentése szerint ‐ azonos, ezért a és b megfelelő együtthatói egyenlők:
1-κα1=α2  és  α1=1-λα2.
Rendezzük és megoldjuk az egyenletrendszert:
κα1+α2=1α1+λα2=1α1=1-λ1-κλ,α2=1-κ1-κλ,
hacsak 1-κλ≠0, ez azonban E és F megválasztása folytán teljesül.
Ezekkel bármelyik előállításából
AH→=(1-κα1)a+α1b=
=1-κλ-κ(1-λ)1-κλa+1-λ1-κλb=(1-κ)a+(1-λ)b1-κλ=GE→1-κλ=μ⋅GE→,
ahol μ puszta szám, csak κ és λ, vagyis az E és F pontnak a BC, DC oldalon való megválasztásától függ. Eszerint az AH→ és GE→ vektorok párhuzamosak.
2. Ha E-t, F-et az oldalak meghosszabbításán választjuk, akkor κ, λ lehet negatív is, vagy 1-nél nagyobb. Ilyenkor előfordulhat, hogy κλ=1, és nem létezik a felhasznált α1, α2 szám. Ez nem bizonyításunk helytelenségére mutat, hanem hogy H nem jön létre.
Példaként bemutatjuk a λ=1/2, κ=2 esetet, DE és BF párhuzamosak (2. ábra).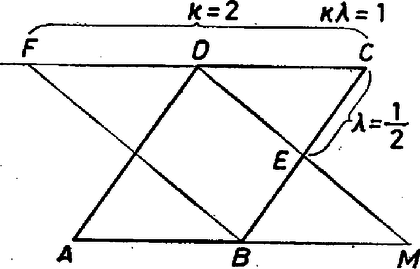
 

2. ábra
 


Megjegyzés. Számos beküldő koordináta-geometriai úton igazolta az állítást. Ez lényegében azonos a II. megoldásnak azzal a speciális esetével, ha ABCD éppen négyzet, majd valamelyik oldal irányában nyújtjuk, másik S síkra vetítjük párhuzamosan, de nem az S-re merőlegesen. Mindez a felhasznált arányokat változatlanul hagyja.