Feladat: F.2349 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Ákosfai Z. ,  Almássy T. ,  Balázs Judit ,  Balázs Z. ,  Béres G. ,  Borsó Zs. ,  Borsosföldi Z. ,  Böröczky K. ,  Csörgő T. ,  Danyi P. ,  Drávucz Katalin ,  Engländer J. ,  Fekete Zs. ,  Fóris Z. ,  Frei Zs. ,  Gulyás Gy. ,  Hajas Csilla ,  Hetyei G. ,  Holbok I. ,  Horváth 713 Z. ,  Horváth A. ,  Kiss 563 P. ,  Lakatos R. ,  Magyar Á. ,  Máray T. ,  Megyesi G. ,  Miskolczi L. ,  Mohay T. ,  Nagy 513 P. ,  Nagy 548 R. ,  Nyikes P. ,  Papp 193 G. ,  Peták T. ,  Prok I. ,  Raffai Zs. ,  Regős Enikő ,  Scharle A. ,  Spanyiel Ilona ,  Szabó E. ,  Szállási Zoltán ,  Szirmai J. ,  Szurok B. ,  Tóth 360 G. ,  Tranta Beáta ,  Törőcsik J. ,  Wágner P. A. ,  Weisz F. 
Füzet: 1982/október, 61 - 62. oldal  PDF  |  MathML 
Témakör(ök): Szabályos sokszög alapú gúlák, Szögfüggvények a térben, Feladat, Trigonometriai azonosságok
Hivatkozás(ok):Feladatok: 1982/január: F.2349

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy konvex poliéder tetszőleges két lapjának hajlásszögén a lapokat tartalmazó, közös határegyenesü félsíkok hajlásszögét értjük. A lapszöget azzal a szöggel mérjük, melynek szárai a lapszög lapjain a határegyenesre merőlegesen helyezkednek el, szögtartománya pedig a lapszög belsejében van. Két lap hajlásszöge 0∘ és 180∘ közé eshet. Feltételezzük, hogy a gúla nem fajul el sem hasábbá, sem síklappá, így 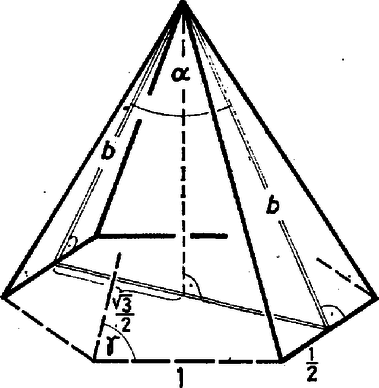0∘<α<180∘ és 0<β<180∘.

 

1. ábra
 

Nyilvánvalóan α vagy β már egymaga meghatározza a szabályos hatoldalú gúla alakját (szögeit), ezért együttes megadásuk a feladatban szükségessé teszi annak vizsgálatát, hogy milyen összefüggésnek kell fennállnia közöttük.
A kérdezett szög természetesen egymáshoz csatlakozó oldalél és alapél hajlásszöge; ez pedig a közös csúcspontból kiinduló, az éleket tartalmazó félegyenesek hajlásszöge, vagyis a félegyenesek által meghatározott két síkbeli szögtartomány közül a nem nagyobbiknak a szöge.
A gúla főcsúcsából kiinduló, a gúla két szemközti oldallapjának az alapélekhez tartozó magasságait tartalmazó félegyenesek hajlásszöge egyenlő α-val (1. ábra). A szabályos hatszög szemközti oldalai ugyanis párhuzamosak, a rájuk illeszkedő oldallapok síkjainak metszésvonala (az oldallapokat tartalmazó félsíkok közös határvonala) is párhuzamos velük, ezért az említett magasságok merőlegesek a két sík metszésvonalára is.
Legyen a gúla alapéle egységnyi. Jelölje b és d az oldallapok alapélhez, ill. oldalélhez tartozó magasságát, c az oldalélek hosszát, γ pedig a keresett szöget.
A szimmetria miatt a gúla magassága felezi az α szöget. α2 ezért egy olyan derékszögű háromszög hegyesszöge, amelynek átfogója b, α2-vel szemközti befogója pedig 32, mivel az egységnyi oldalú szabályos hatszög szemközti oldalainak távolsága 3. Ezek szerint
b=32sinα2,
γ viszont egy olyan derékszögű háromszög hegyesszögének tekinthető, amelynek γ-val szemközti befogója b, másik befogója 12. Ebből következik, hogy
tgγ=2b=3sinα2.
Mivel 0∘<α2<90∘ és γ hegyesszög, megállapítható, hogy 60∘<γ<90∘.
Keressünk most β és γ között kapcsolatot. Tekintsük a gúla két szomszédos oldallapjának a közös oldalélhez tartozó magasságát. A szimmetria miatt ezek talppontjai egybeesnek. A lapok hajlásszögéről mondottak alapján e magasságok egy β nagyságú szög szárainak kezdő szakaszai. Abban az egyenlő szárú háromszögben, amelynek alapja 3, szárai pedig d hsszúságúak, a szárak által bezárt szög 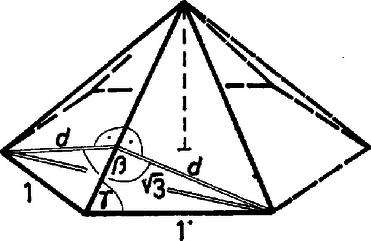β.
 

2. ábra
 

Így
d=32sinβ2.
Ennek alapján
sinγ=d=32sinβ2.
Mivel 32<d<1, ezért 120∘<β<180∘. γ-ra természetesen itt is azt kapjuk, hogy 60∘<γ<90∘.
Kézenfekvő, hogy az α és β közötti összefüggést a γ-ra kapott képletekből állapítsuk meg.
Mivel γ hegyesszög,
sinγ=tgγ1+tg2γ.
Ennek alapján
32sinβ2=3sinα21+3sin2α2.
Azonos átalakítások révén ‐ figyelembevéve, hogy α2 és β2 hegyesszögek ‐ a következő összefüggésekre juthatunk:
sin2α2+3=4sin2β2,
vagy
cosα2=2cosβ2.

Szállási Zoltán (Esztergom, Dobó K. Gimn., IV. o. t.)