Feladat: F.2347 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1982/október, 57 - 58. oldal  PDF  |  MathML 
Témakör(ök): Húrnégyszögek, Feladat
Hivatkozás(ok):Feladatok: 1982/január: F.2347

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az ABCD négyszög köré írt kört k-val, az OAB és OCD háromszögek köré írt köröket k1-gyel és k2-vel. Vizsgáljuk először azt az esetet, amikor az AB, CD egyenesek metszik egymást, és egyikük sem átmérője k-na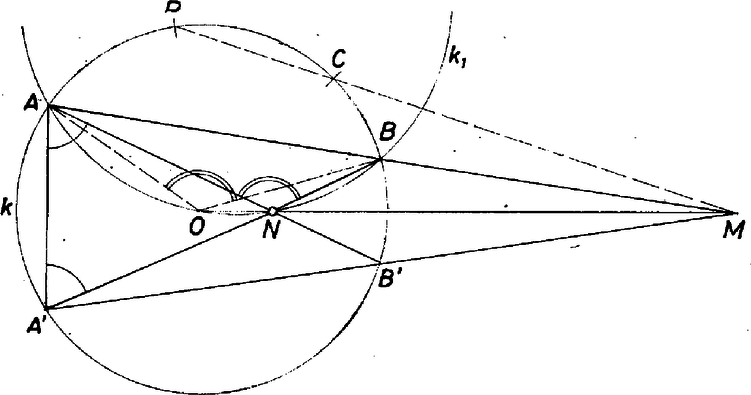k.



Jelöljük az AB, CD egyenesek metszéspontját M-mel. Mivel az ABCD négyszög konvex, M a k-n kívül van. Tükrözzük A-t és B-t az MO egyenesre, és jelöljük a tükörképeket A'-vel, B'-vel, az ABB'A' szimmetrikus trapéz átlóinak metszéspontját pedig N-nel. N nem lehet azonos O-val, hiszen ekkor AB, A'B' és CD párhuzamosak lennének. A tükrözés miatt az AA'N háromszög egyenlő szárú, és az AA' alapján levő szögeinek összege egyenlő a háromszög ANB külső szögével. Az AB szakasz tehát az AB egyenes azonos oldalán levő O és N pontokból egyenlő szögek alatt látszik, hiszen mindkét szög egyenlő az AA'B szög kétszeresével. (Az AOB szög az AA'B kerületi szöghöz tartozó középponti szög.) Emiatt N rajta van k1-en, és a körhöz külső pontból húzott szelők darabjaira vonatkozó ismert összefüggés szerint
MA⋅MB=MO⋅MN.(1)

Ha most a CD szakaszt is tükrözzük az MO egyenesre, és a CDD'C' trapéz átlóinak a metszéspontját L-lel jelöljük, akkor hasonlóan kapjuk, hogy
MC⋅MD=MO⋅ML.(2)
Mivel (1) és (2) bal oldalán a k kör két M-en átmenő szelőjének a darabjait szoroztuk össze, e szorzatok egyenlőek, tehát MN=ML. Az N és L pontok k-beli trapézok átlóinak a metszéspontjai, tehát az MO egyenesen az M-nak ugyanazon az oldalán vannak, így N és L csak azonos lehet. Mivel N a k1-en, L a k2-n van, e pontok Q-val is azonosak. (Láttuk,, hogy N és L az O-tól különböző pontok.) A feladat állítása ezek után a k kör Q-n átmenő AB', CD' húrjaira vonatkozó
AQ⋅QB'=CQ⋅QD'
összefüggés következménye.
 

Ha az AB egyenes k átmérője, akkor k1 szerepét az AB egyenes veszi át, és az állítás a fenti bizonyítással együtt lényegében érvényben marad. Ha AB és CD párhuzamosak, akkor az O-n átmenő, velük párhuzamos egyenes érinti a k1, k2 köröket, azok tehát egymást is érintik. Így ebben az esetben Q azonos O-val, és az állítás nyilvánvaló.