Kezdőlap


Feladat:	F.2324	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csikós Zs. , Danyi P. , Drávucz Katalin , Fritz P. , Havasi G. , Hetyei G. , Holbok I. , Ittzés A. , Károlyi Gy. , Kovács 285 P. , Magyar Á. , Markó T. , Mikó Teréz , Nádor P. , Peták T. , Szemők Á. , Szöllősi Gabriella , Tóth 360 G. , Tranta Beáta , Törőcsik J. , Virányi L.
Füzet:	1982/február, 66 - 67. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Szabályos tetraéder, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1981/szeptember: F.2324

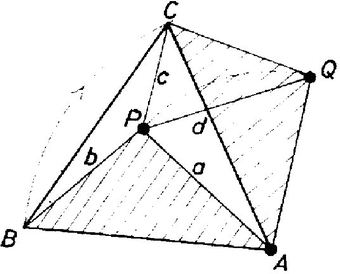
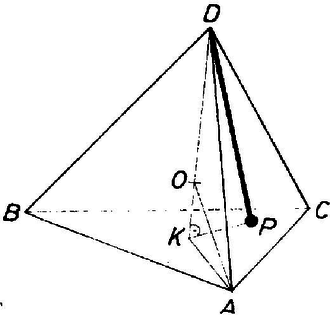
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a $P A$ , $P B$ , $P C$ hosszúságokat rendre $a$ -val, $b$ -vel, $c$ -vel. Forgassuk el $A$ körül az $A B P$ háromszöget úgy, hogy $B$ a $C$ -be kerüljön, és jelöljük $P$ új helyzetét $Q$ -val. Mivel az $A B C$ háromszög szabályos, az $A P Q$ háromszög is az. Így a $C P Q$ háromszög oldalainak a hossza épp a három adott távolság. Ebből egyrészt következik, hogy a feladat csak akkor oldható meg, ha az $a$ , $b$ , $c$ oldalakkal háromszög szerkeszthető, másrészt a $P Q = a$ , $Q C =$ $= b$ , $C P = c$ oldalakkal rajzolt háromszög $P Q$ oldala fölé kifelé rajzolt $A P Q$ szabályos háromszög $A$ csúcsa a $C$ -vel együtt meghatározza az $A B C$ háromszög $A C$ oldalát. Jelöljük ezt $d$ -vel. A koszinusz tételt először az $A P C$ , majd a $C P Q$ háromszögre alkalmazva kapjuk, hogy

\begin{matrix} d^{2} & = a^{2} + c^{2} - 2 a c cos (60^{\circ} + β) = a^{2} + c^{2} - 2 a c (\frac{1}{2} cos β - \frac{\sqrt[]{3}}{2} sin β) = \\ = a^{2} + c^{2} - \frac{1}{2} (a^{2} + c^{2} - b^{2}) + \sqrt[]{3} a c sin β = \frac{1}{2} (a^{2} + b^{2} + c^{2}) + 2 \sqrt[]{3} t, \end{matrix}

ahol

β

C P Q

szöget,

t

C P Q

háromszög területét jelöli.
Jelöljük még

D

-nek az

A B C

síkon levő vetületét

K

-val. Pitagorasz tétele alapján

P D^{2} = P K^{2} + K D^{2}

. Ez utóbbi

d

alapján könnyen meghatározható, hiszen ha a tetraéder centrumát

O

-val jelöljük, akkor

O

negyedeli a

D K

szakaszt, és

A O = O D

. Emiatt az

A K O

háromszögben

\begin{matrix} {(\frac{3}{4} D K)}^{2} = {(\frac{1}{4} D K)}^{2} + A K^{2}, \end{matrix}

tehát

D K^{2} = 2 A K^{2} = \frac{2}{3} d^{2}

. Belátjuk, hogy

\begin{matrix} P K^{2} = \frac{a^{2} + b^{2} + c^{2}}{3} - A K^{2}, \end{matrix}

(1)

amiből kapjuk, hogy

\begin{matrix} P D^{2} = \frac{a^{2} + b^{2} + c^{2}}{3} - \frac{d^{2}}{3} + \frac{2 d^{2}}{3} = \frac{1}{3} (a^{2} + b^{2} + c^{2} + d^{2}) = \\ = \frac{1}{2} (a^{2} + b^{2} + c^{2}) + \frac{2 t}{\sqrt[]{3}} . \end{matrix}

Ismeretes, hogy az

a

b

c

oldalú háromszög területére

\begin{matrix} 16 t^{2} = (a + b + c) (a + b - c) (a - b + c) (- a + b + c) = 2 (a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2}) - (a^{4} + b^{4} + c^{4}) \end{matrix}

teljesül, tehát

\begin{matrix} P D^{2} = \frac{1}{2} (a^{2} + b^{2} + c^{2}) + \frac{1}{2 \sqrt[]{3}} \sqrt[]{2 (a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2}) - (a^{4} + b^{4} + c^{4})} . \end{matrix}

(2)

Be kell még látnunk az (1) összefüggést. Válasszuk a koordináta-rendszer origójának a

K

pontot, és jelöljük a szóban forgó pontok koordinátáit a megfelelő kisbetűkkel és egyes, illetve kettes indexszel. Így kapjuk, hogy

\begin{matrix} P K^{2} = p_{1}^{2} + p_{2}^{2}, \\ a^{2} = {(a_{1} - p_{1})}^{2} + {(a_{2} - p_{2})}^{2}, \\ b^{2} = {(b_{1} - p_{1})}^{2} + {(b_{2} - p_{2})}^{2}, \\ c^{2} = {(c_{1} - p_{1})}^{2} + {(c_{2} - p_{2})}^{2}, \\ A K^{2} = a_{1}^{2} + a_{2}^{2} . \end{matrix}

Ezeket (1)-be helyettesítve, és figyelembe véve, hogy

A K^{2} = B K^{2} = C K^{2}

a_{1} + b_{1} + c_{1} = 0

a_{2} + b_{2} + c_{2} = 0

, valóban azonosságot kapunk. Az utóbbi két összefüggés azért igaz, mert

K

A B C

háromszögben nemcsak a körülírt kör középpontja, de súlypont is.

Megjegyzés. Az

a

b

c

d

szakaszok közti összefüggés szimmetrikus alakra hozható:

\begin{matrix} {(a^{2} + b^{2} + c^{2} + d^{2})}^{2} = a^{4} + b^{4} + c^{4} + d^{4} . \end{matrix}