Kezdőlap


Feladat:	F.2307	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1981/október, 53 - 55. oldal		PDF \| MathML
Témakör(ök):	Beírt gömb, Szabályos sokszög alapú gúlák, Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 1981/március: F.2307

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az alaplap (szabályos ötszög) csúcsait rendre $A$ , $B$ , $C$ , $D$ , $E$ -vel, a gúla hatodik csúcsát $F$ fel. Mivel az oldallapok leforgatásával szabályos csillagötszög keletkezik, azért $F$ -nek az $A E$ él körüli leforgatott helyzete az $A B$ és $E D$ oldalegyenesek metszéspontjába esik (1. ábra).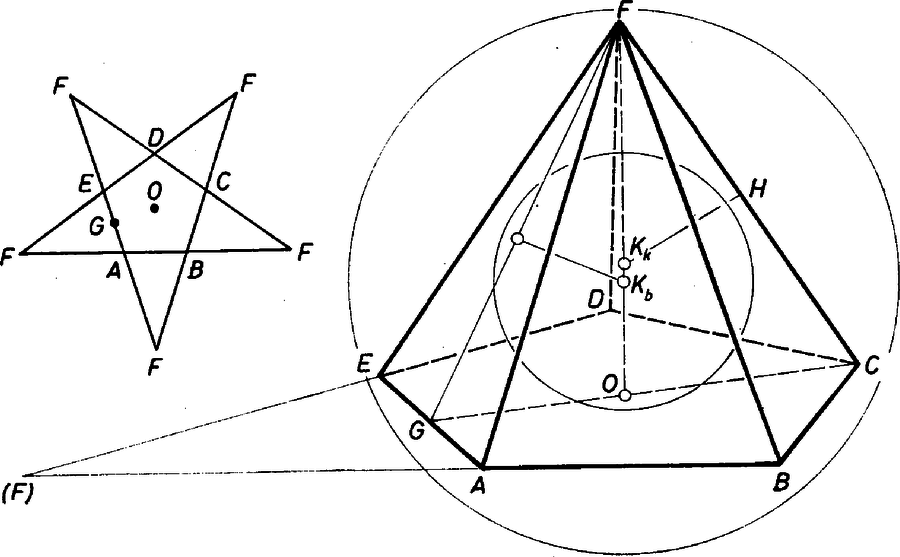

1. ábra

E szerint az oldallapok olyan egyenlő szárú háromszögek, amelyekben az alapon levő szög

72^{\circ}

, és az oldalélek hossza

\begin{matrix} A F = \frac{A E / 2}{cos F A E ∢} = \frac{1}{2 cos 72^{\circ}} = \frac{1}{2 sin 18^{\circ}} = \frac{2}{\sqrt[]{5} - 1} = \frac{\sqrt[]{5} + 1}{2} (= 1,618 egység) . \end{matrix}

Jelöljük az alaplap középpontját

O

-val ‐ ez a magasság talppontja ‐, az

A E

él felezőpontját

G

-vel. A gúla előírt szabályosságából következik, hogy mindkét gömb középpontja az

F O

magasságvonalon (forgási szimmetriatengelyen) lesz, továbbá a beírt gömb az alaplapot

O

-ban érinti, az

A E F

lapot pedig a

G F

oldalmagasság egy pontjában.
Legyen még a beírt gömb középpontja

K_{b}

, és sugara

ϱ

, így

K G_{b}

felezi az

F G O ∢ = γ

szöget, és

\begin{matrix} ϱ = O K_{b} = G O tg \frac{γ}{2} = G O \sqrt[]{\frac{1 - cos γ}{1 + cos γ}} . \end{matrix}

Itt ismert goniometriai összefüggések alapján, valamint felhasználva

18^{\circ}

-nak és többszöröseinek a szabályos ötszögből kiszámítható szögfüggvényeit, egyrészt

\begin{matrix} G O = A G tg 54^{\circ} = \frac{1}{2} \sqrt[]{\frac{5 + 2 \sqrt[]{5}}{5}} = \frac{1}{2} \sqrt[]{1 + \frac{2}{\sqrt[]{5}}}, \end{matrix}

másrészt

cos γ = G O / G F

, így a gyökjel alatti kifejezés:

\begin{matrix} \frac{1 - cos γ}{1 + cos γ} = \frac{G F - G O}{G F + G O} = \frac{G A (tg 72^{\circ} - tg 54^{\circ})}{G A (tg 72^{\circ} + tg 54^{\circ})} = \frac{sin 18^{\circ}}{sin 3 \cdot 18^{\circ}} = \frac{1}{3 - 4 sin^{2} 18^{\circ}} \\ = \frac{2}{3 + \sqrt[]{5}} = \frac{3 - \sqrt[]{5}}{2} . \end{matrix}

Ezekkel

\begin{matrix} ϱ = \frac{1}{2} \sqrt[]{\frac{5 + 2 \sqrt[]{5}}{5}} \cdot \frac{3 - \sqrt[]{5}}{2} = \sqrt[]{\frac{5 + \sqrt[]{5}}{40}} (= 0,4253 egység) . \end{matrix}

A körülírt gömb

R

sugarának számításához a

C O F

háromszöget használjuk. Jelöljük a gömb középpontját

K_{k}

-val,

F C

felezőpontját

H

-val. Az

F K_{k} H

és

F C O

derékszögű háromszögek hasonlóságából

\begin{matrix} \frac{F H}{R} = \frac{F O}{F C}, R = \frac{F C^{2}}{2 \cdot F O} = \frac{F C^{2}}{2 \sqrt[]{F C^{2} - O C^{2}}} . \end{matrix}

Itt

\begin{matrix} O C = O A = \frac{A G}{cos 54^{\circ}} = \frac{1}{2 sin 36^{\circ}} = \frac{2}{\sqrt[]{10 - 2 \sqrt[]{5}}} = \sqrt[]{\frac{5 + \sqrt[]{5}}{10}} . \end{matrix}

A nevezőbeli négyzetgyökjel alatt

\begin{matrix} F C^{2} - O C^{2} = {(\frac{\sqrt[]{5} + 1}{2})}^{2} - \frac{5 + \sqrt[]{5}}{10} = \frac{1}{5 - 2 \sqrt[]{5}} \end{matrix}

áll, végeredményben tehát

\begin{matrix} R = \frac{1}{4} \sqrt[]{10 + 2 \sqrt[]{5}} (= 0,9511 egység) . \end{matrix}

Megjegyzés. Két észrevételt teszünk számításaink alapján. Egyrészt

R / ϱ = \sqrt[]{5}

, másrészt

\begin{matrix} F O = \frac{F C^{2}}{2 R} = \sqrt[]{1 + \frac{2}{\sqrt[]{5}}} = R + ϱ, \end{matrix}

tehát

K_{b}

és

K_{k}

egybeesik.

II. megoldás (vázlat). Induljunk ki a szabályos ötszög eukleidészi szerkesztéséből (2. ábra).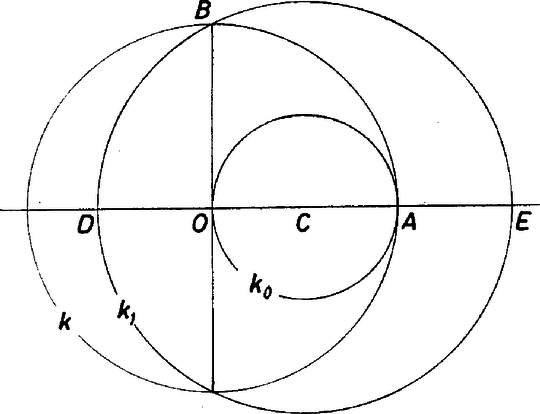

2. ábra

Legyenek

O A

és

O B

k

kör merőleges sugarai,

C

O A

szakasz felezőpontja, és jelöljük a

C

középpontú,

A

-n, illetve

B

-n átmenő köröket

k_{0}

-lal, illetve

k_{1}

-gyel,

k_{1}

-nek az

O A

egyenesen levő pontjait

D

-vel,

E

-vel (

D

legyen közülük

O

-hoz közelebb). Az

E B D

derékszögű háromszögben

B O

D O

O E = O A + A E = O B + D O

szakaszok mértani közepe, emiatt

\begin{matrix} D O : O B = O B : (O B + D O), \end{matrix}

vagyis

D O

és

O B

aránya megegyezik a szabályos tízszög oldalainak és a köré írt kör sugarának az arányával. Így

D O

valóban a

k

-ba írt szabályos tízszög oldala, és

\begin{matrix} B E^{2} = D E \cdot O E \end{matrix}

miatt

B E

k

-ba írt szabályos ötszög átlója, végül

D B : B E = D O : O B

miatt

D B

k

-ba írt szabályos ötszög oldala.
Forgassuk meg ezt az ábrát a

D E

egyenes körül, és jelöljük a

k_{0}

k_{1}

körök forgatásából keletkező gömböket

G_{0}

lal,

G_{1}

-gyel.

G_{1}

-ből a

B O

forgatásából származó sík

k

-val egybevágó kört metsz ki, tehát az ebbe írt szabályos ötszög oldalai

B D

-vel egyenlőek, átlói pedig

B E

-vel. így ez az ötszög

E

-vel együtt épp a feladatban szereplő gúlát határozza meg, ha

B D

egységnyi.
A kapott gúlának

G_{1}

természetesen a köré írt gömbje, megmutatjuk, hogy

G_{0}

a beírt gömb. A konstrukció miatt

G_{0}

érinti az alaplapot, melyben például a

B

csúcsból induló átlók az oldallapokkal egybevágó háromszögeket zárnak közre. Mivel

B C = E C

, a

G_{0}

-hoz

E

-ből húzott érintősíkok is

k

-val egybevágó köröket metszenek ki

G_{1}

-ből, tehát a gúla oldallapjai valóban érintik

G_{0}

-t.
Ha

O C = ϱ

, akkor

B C = ϱ \sqrt[]{5}, D O = ϱ (\sqrt[]{5} - 1), D B^{2} = ϱ^{2} (10 - 2 \sqrt[]{5})

. Ha tehát

D B = 1

, akkor

\begin{matrix} ϱ^{2} = \frac{1}{2} \frac{1}{5 - \sqrt[]{5}} = \frac{5 + \sqrt[]{5}}{40} . \end{matrix}

Így a gúlába írt gömb sugara

ϱ = \sqrt[]{\frac{5 + \sqrt[]{5}}{40}}

és a gúla köré írt gömb sugara

B C = ϱ \sqrt[]{5} = \sqrt[]{\frac{5 + \sqrt[]{5}}{8}}