Feladat: F.2300 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Ákosfai Z. ,  Böröczky K. ,  Dósa Gy. ,  Erdélyi E. ,  Gulyás Gy. ,  Hetyei G. ,  Ittzés A. ,  Károlyi Gy. ,  Kerényi I. ,  Kurucz Gy. ,  Lenkó Cs. ,  Mikó Teréz ,  Regős Enikő ,  Simonyi G. ,  Terenyi Z. ,  Tranta Beáta 
Füzet: 1981/november, 123 - 126. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai számítások trigonometria nélkül négyszögekben, Négyszögek szerkesztése, Feladat, Középponti és kerületi szögek
Hivatkozás(ok):Feladatok: 1981/február: F.2300

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatra csak azzal a föltételezéssel adunk megoldást, hogy az eredeti ‐ a megszerkesztendő ‐ EFGH négyszög átlói M metszéspontjának mind a négy vetülete az illető oldalszakaszon keletkezett, a HE oldalon az adott A csúcs, és tovább a B, C, D (1. á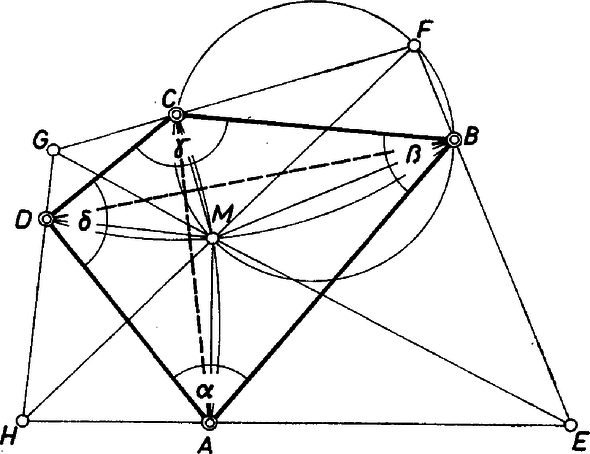bra).

 

1. ábra
 

Föltételezésünk egyáltalán nem következik abból, hogy az ABCD négyszög konvex.
Az kényszerít a fenti föltételezésre, hogy négyszögszerkesztéseknél jóval bonyolultabb lehet a diszkusszió, mint háromszögszerkesztéseknél, különösen ha ‐ mint most is ‐ nem méretek állnak rendelkezésre, hanem pontok helyzete ismert. (Gyakorlatilag fontos esetben tehát a vetületek elhelyezkedésére változatokat is figyelembe kellene vennünk, és esetenként vizsgálnunk, hogy ezáltal milyen változások következnek be az alábbiakban.)
A feladatra rátérve, elemzésünkben szokás szerint föltesszük, hogy már sikerült megoldani. Az adott négyszög szögei alapján két mértani helyet ‐ látókörívet ‐ szerkeszthetünk a kérdéses M pontra. Ennek ismeretében az MA, MB, MC, MD szakaszokra a talppontjukon át állított merőlegesek adják meg a keresett négyszög oldalegyeneseit, és amennyiben ezek szomszédos páronként metszik egymást, akkor maga a négyszög is létrejön.
Ábránkon a BD egyenes elválasztja M-et és C-t, így ABCD konvex volta alapján A viszont az M-et tartalmazó partján van BD-nek. Ezért a C-t tartalmazó BMD szögtartomány konvex, az A-t tartalmazó BMD szögtartomány konkáv. Mindkettőnek részét teszi az eredeti átlók közti FMG, illetve HME szög, és a többletet ki lehet fejezni az adott négyszög C-nél és A-nál levő szögeivel.
Feltevésünk szerint MAEB, MBFC, MCGD és MDHA konvex húrnégyszögek, mert 2-2 szemben fekvő szögük derékszög. Ezekből előbb a konvex, majd a konkáv BMD szögre
ω=BMD∢=FMG∢+BMF∢+GMD∢==FMG∢+BCF∢+GCD∢==FMG∢+(180∘-BCD∢),
hasonlóan
360∘-ω=HME∢+DMH∢+EMB∢==FMG∢+(180∘-DAB∢),
ezt az előbbiből kivonva, rendezés után
ω=180∘-12(BCD∢-BAD∢)=180∘-γ-α2,(1)
ekkora tehát a BD átlónak a keresett M-ből vett látószöge.
A BD szakasznak M-ből vett "másik'' látószöge viszont 360∘-ω=180∘-(α-γ)/2, vagyis az MB és MD félegyenesek között az a szögtartomány, amelyik A-t tartalmazza. Ezek szerint ‐ ha kizárólag az A, B, C, D pontokat ismerjük, az ω, ill. 360∘-ω nyílású látószögkörívet a BD-nek azon a partján kell szerkesztenünk, amelyiken a BD-re ránéző szögek közül a kisebbiknek a csúcsa van.
Ha α=γ, akkor a kapott feltétel azt jelenti, hogy M és BD szakaszon van.
Hasonlóan a konvex AMC látószögre
φ=AMC∢=180∘-12(ADC∢-ABC∢)=180∘-δ-β2,
mert felvételünkben δ>β és a CA körív a B partján rajzolandó.
Ezekből a fönt leírt szerkesztés végrehajtható. ω>α, vagyis nagyobb, mint BD-nek A-ból vett látószöge, hiszen
ω-α=180∘-γ+α2>0,
ezért a BD látókörív elválasztja egymástól A-t és C-t (és ugyanígy φ>β), a két körív metszi egymást, M létrejön.
Megmutatjuk, hogy a két látókörív M metszéspontjából és az MA, ... szakaszokra a talppontjukon át állított merőlegesekből kapott négyszögben ‐ ha az létrejött ‐ az átlók valóban átmennek M-en. Ekkor a fönti elemzésben felhasznált húrnégyszögek immár szerkesztésünknél fogva húrnégyszögek. Ekkor tehát
FMG∢=BMD∢-(BMF∢+GMD∢)==BMD∢-(BCF∢+GCD∢)==(180∘-γ-α2)-(180∘-γ)=γ+α2,
másrészt hasonlóan
GMH∢=GMA∢-(CMG∢+HMA∢)==CMA∢-(CDG∢+HDA∢)==(180∘-δ-β2)-(180∘-δ)=δ+β2,
tehát
FMG∢+GMH∢=12(γ+α+δ+β)=180∘,
M rajta van az FH átlón. Ugyanígy látható be, hogy M a GE átlón is rajta van. Ezek szerint az EFGH négyszögből a feladatban leírt úton valóban visszakapjuk az ABCD négyszöget.
Hangsúlyozzuk: ebben a bizonyításban is használtuk ábránkat, a pontjaink helyzetére használt föltételezéseinket. Egy más eredményre vezető helyzet hasonló kidolgozása látható a 2. ábrá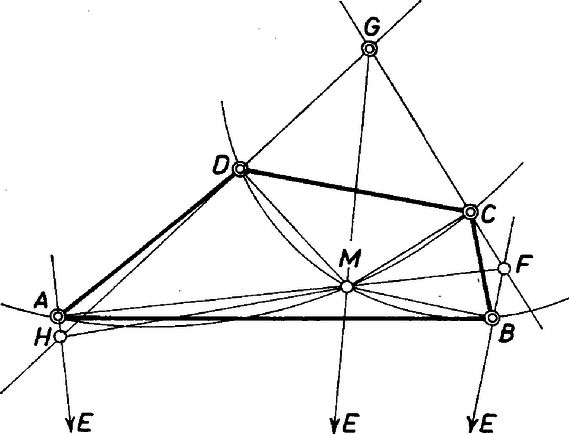n.
 

2. ábra
 

 

Megjegyzés. Érkezett olyan dolgozat, amely az ABCD négyszögből kiindulva állít elő a leírt úton újabb négyszöget, és ezt ismétli többször "addig, amíg a kérdéses négyszöghöz hasonlót nem kap''.
Egy kérdés: mivel a kérdéses ‐ azaz keresett ‐ négyszöget nem ismerjük, miből veszi észre a dolgozat beküldője, hogy hasonlót kapott hozzá valamelyik ismétlés eredményeképpen?
Igazságérzetünk is tiltakozik. Ha egyáltalán volna valamiféle "hasonlóságbiztosító'' átöröklés, annak része lenne, hogy pl. a H szögből ki lehessen fejezni A, B, C, D valamelyikét, majd a származékok valamelyik szögét, és kellő számú lépés után a H szög valahol megismétlődnék. Két négyszög hasonlóságához azonban nem elegendő a szögek páronkénti megegyezése! (Hasonló-e két téglalap?) És ha a H szög nagyságát történetesen mégis örökölné pl. az A szög, mit szólna ehhez a D szög, amely éppolyan szomszéd, mint az A? És hasonlóan B és C is egyformán fekszenek H-hoz képest, mert idomunk csúcsainak, szögeinek a száma páros. Igazságos volna-e?
Háromszög egy ilyenféle származékánál valóban lehetne valamiféle örököst kijelölni: a szemben fekvőt, ahogy pl. a γ szögnek a megfelelője a talpponti háromszögben 180∘-2γ, ill. 2γ-180∘ (aszerint, hogy γ hegyes, ill. tompaszög). Még az is előfordulhat, hogy egy háromszög első vagy második, ... , n-edik talpponti háromszöge hasonló az eredetihez. Vályi Gyula kolozsvári egyetemi tanár foglalkozott ezzel a problémával. De ehhez szükséges, hogy a háromszög mindegyik szöge racionális hányadrésze legyen a 180∘-nak (a szögösszegnek). Még ez a távoli hasonlat sem ad hát támasztékot az idézett kijelentéshez, sejtéshez.