Kezdőlap


Feladat:	F.2293	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Tranta Beáta
Füzet:	1981/szeptember, 12 - 15. oldal		PDF \| MathML
Témakör(ök):	Egyéb szinezési problémák, Teljes indukció módszere, Feladat, Egyéb sokszögek geometriája
Hivatkozás(ok):	Feladatok: 1981/január: F.2293

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy a kívánt felbontás minden $n \geq 3$ értékre megvalósítható. Hozzátesszük mindjárt: abban az értelemben, hogy a részháromszögek csúcsai nemcsak az eredeti sokszög csúcsaiban lehetnek. (A feladat nem tartalmazott ilyen megkötést, azonban többen úgy értelmezték.)
Legyen a felbontandó $A_{1} A_{2} ... A_{n}$ konvex $n$ -szög legkisebb oldalának $1 / 3$ része $h$ , mérjük föl ezt minden csúcstól a szomszédos csúcsok irányába, és jelöljük a végpontot $A_{i}$ -től a körüljárás irányában $B_{i}$ -vel, az ellentétes irányban $C_{i}$ -vel, $i = 1,2, ... n$ (1. ábra).

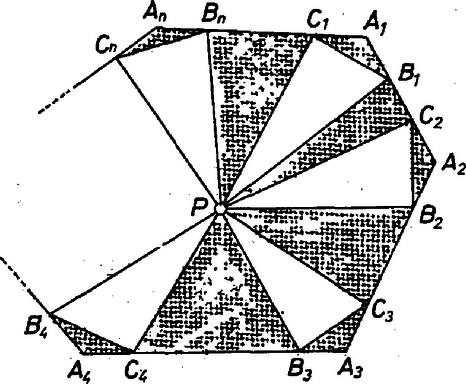1. ábra

A_{i} B_{i} C_{i}

háromszögeket csak feketére festhetjük, a még festetlen konvex

2 n

-szög

C_{i} B_{i}

oldalaira a felbontásban fehér (világos) háromszögeknek kell támaszkodniuk, a

B_{i} C_{i + 1}

oldalaira pedig sötét háromszögeknek (

C_{n + 1}

-en természetesen

C_{1}

-et értjük).
Ezt egy csapásra megvalósíthatjuk úgy, hogy mindezen pontokat összekötjük egy, a

2_{n}

-szög belsejében választott

P

ponttal, és a keletkezett háromszögeket a

C_{i} B_{i}

, ill.

B_{i} C_{i + 1}

oldalukra megállapított színűre festjük. ‐ A felbontás és színezés nyilván megfelel az előírásnak. (A rész háromszögek száma itt

f_{n} = 3 n

Tranta Beáta (Miskolc, Földes F. Gimn., III. o. t.)

II. megoldás.

n

szerinti teljes indukcióval bizonyítjuk az I. megoldásban kimondott állítást, továbbra is az ott kimondott értelmezéssel.

n = 3

esetén a háromszöget feketére festve kapunk megfelelő megoldást.
Tegyük föl, hogy konvex

n

-szögre igaz az állításunk, tekintsük az

A_{1} A_{2} ... A_{n} A_{n + 1} = P_{n + 1}

konvex

(n + 1)

-szöget. Jelölje

B_{i}

A_{i} A_{i + 1}

oldal egy belső pontját,

i = 2,3, ..., n

(2. ábra).

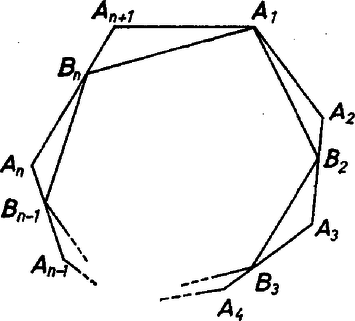2. ábra

Ekkor az

A_{1} B_{2} B_{3} ... B_{n} = Q_{n} n

-szög konvex, bele van írva

P_{n} + 1

-be, csak csúcspontjai vannak

P_{n + 1}

kerületén. Tekintsük

Q_{n}

-nek egy, az indukciós feltevés szerint létező felbontását, de cseréljük föl benne a fekete és a fehér színt. Végül

P_{n + 1}

-nek a

Q_{n}

által le nem fedett részét feketére festve, a

P_{n + 1}

-nek egy megfelelő felbontását kapjuk.
Eszerint minden konvex sokszög felbontható a kívánt módon. (

P_{n + 1}

leírt kibontása a

Q_{n}

felbontásához képest

n

új háromszöget tartalmaz.)

Megjegyzések. 1. Kissé fonákul hat, hogy a teljes indukciós bizonyítás elindításában ,,1 részre bontunk'', amit így is lehet mondani: nem bontunk. Gyakori azonban, hogy ilyen bizonyításokban a kiindulás többé‐kevésbé elfajult eset, vagy csak mesterkélt értelmezés mellett mutat példát. Az erre az

f_{3} = 1

-re a fentiek szerint kialakított

f_{4} = f_{3} + 3 = 4

felbontás azonban már valódi bontás (3. ábra), és ilyen

n = 3

-ra is van (4. ábra), ebben is

f_{3} = 4

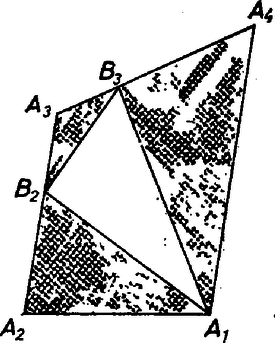3. ábra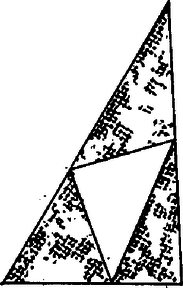

4. ábra

2. A továbbhaladásnak más természetű ,,szépséghibája'', hogy rohamosan nő

n

-nel az

f_{n}

szám,

f_{n + 1} = f_{n} + n

alapján

f_{5} = 8, ... f_{8} = 26 > 3 \cdot 8

(amit az I. megoldásban láttunk). Márpedig ,,íratlan szépségideálja'' számos feladattípusnak a lehetőleg kis létszám, a felépítés (a ,,konstrukció'') egyszerűsége.
Mutathatunk azonban olyan módosítást, amelyben tetszetős végeredmény fejlődik ki szemeink előtt. Arra alapul ez, hogy az

n = 5

és

n = 6

esetekre az

n = 4

eseténél egyre szebb olyan felbontások adhatók, még hozzá éppen a 3. ábrából, amelyekben

f_{5} = f_{6} = f_{4} = 4

. Erre tekintettel közös továbbfejlesztés adható páratlan és páros

n

-ekre. Sőt ez is javítható lesz.
A 3. ábrán

B_{3}

-at

A_{4}

-be tolva elfajul a

B_{3} A_{4} A_{1}

háromszög, fehér oldala keletkezik a négyszögnek, és erre egy fekete háromszöget illesztve, az

n = 5

esetre kapunk megoldást (5. ábra, a szaggatott vonaltól balra eső rész). Az odarajzolt

A_{1} A_{4} A_{5}

háromszöggel fenntarthatjuk a konvexséget; tovább is ilyen ,,odatapasztásokat'' végzünk majd.

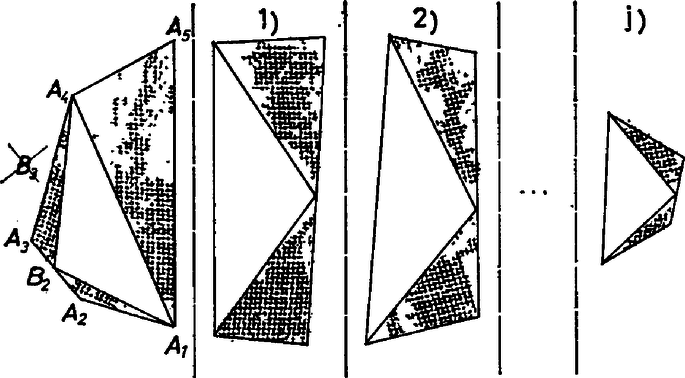5. ábra

Még szebb az

n = 6

eset:

B_{2}

-t

A_{3}

-ba toljuk és az elfajult háromszöget a fekete

A_{3} A_{4} A *

-gal pótoljuk (6. ábra), még mindig

f_{6} = 4

, és minden eddigivel szemben kizárólag átlók révén való felbontás áll előttünk.

6. ábra

Nevezzük el most az 5. ábra

A_{1} A_{2} A_{3} A_{4}

négyszögét oldalszámnövelő tapasz-nak,

3

oldala fekete,

1

fehér. Ennek ismételt odarajzolásával az 5‐6. ábrákból (a szaggatott vonalon túl, de tulajdonképpen bármelyik szélső fekete háromszögön túl) egyformán kaphatunk felbontást‐színezést az

n = 5 + 2 j

és

n = 6 + 2 j

esetekre,

j = 1,2, ...

.
Minden egyes ilyen tapasz

2

új csúcsot hoz be a ,,felbontandó'' sokszögbe, így a felbontások háromszögeinek száma

f_{5 + 2 j} = f_{6 + 2 j} = 4 + 3 j

, ahol

2 j = n - 5

, ill.

2 j = n - 6

.
Már csak annak észrevétele van hátra, hogy képezhető

4

-nél több oldalú oldalszámnövelő tapasz is, sőt az

5

oldalú tapasz ,,szebb'', mint a

4

oldalú (7.ábra), mert kizárólag átlók útján bont. Emiatt nem is érdemes már másra gondolni.

7. ábra

Most már a 3., 5. és 6. ábrák ilyen továbbfejlesztésére gondolunk, minden tapasz

3

új csúcsot hoz és

3

új háromszöget, mindig

\begin{matrix} f_{n} = f_{4 + 3 j} = f_{5 + 3 j} = f_{6 + 3 j} = 4 + 3 j, \end{matrix}

innen

3 j = n - 4

, ill.

n - 5

, ill.

n - 6

\begin{matrix} f_{n} = {\begin{matrix} n, & ha n = 3 k + 1 alakú, \\ n - 1, & ha n = 3 k + 2 alakú, \\ n - 2, & ha n = 3 k alakú . \end{matrix} \end{matrix}

f_{3 k} = 3 k - 2

eredmény semmi esetre sem javítható, hiszen a

3 k

-szög (belső) szögeinek összege

(3 k - 2) \cdot 180^{\circ}

, és minden belső szögnek egészben vagy részekre bontva ott kell lennie a részháromszögek szögeinek együttesében.
A 8. ábra

n = 9

-re mutatja az előzőek szerinti felbontást, ez

7

rész. (Szabályos

9

-szögre ez az egyetlen ilyen felbontás,^{$^{*}$} a szabályos

12

-szög ilyen feldarabolásainak száma^{$^{*}$} pedig

4

. A szabályossággal persze már méretes és szimmetriaviszonyokat is tekintetbe vettünk.)

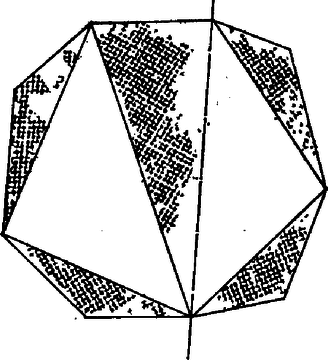8. ábra

3. Egy

3 k

oldalszámú konvex sokszögnek a legutóbbiak szerinti, kizárólag átlók révén való felbontásáról az is kimondható, hogy minden csúcsa páratlan sok részháromszögnek csúcsa, hiszen a csúcsokban a háromszögek váltakozva feketék és fehérek, és az utolsó is fekete, vagy pedig csakis

1

fekete háromszög tartozik a csúcshoz.
Itt kapcsolódunk a feladat szövegének mikénti értelmezéséhez, amelyet már említettünk az I. megoldás elején. Kizárólag átlókat felhasználva a bontásban ‐ és persze egymást nem metsző átlókat, különben ugyanis nem tekinthető át a részek alakja ‐, csak az

n = 3 k

oldalszámú konvex sokszögeknek van a feladat kimondott követelményeit kielégítő felbontása - színezése. ‐ Ez azonban nem a fentiekből következik. Egyébként az 1967. évi Kürschák József matematikai tanulóverseny 2. feladata ez volt: ,,Egy konvex sokszöget egymást nem metsző átlók háromszögekre bontanak fel. A sokszög minden csúcsa páratlan sok ilyen háromszög csúcsa. Bizonyítsuk be, hogy a sokszög oldalainak száma

3

-mal osztható.''^{$^{*}$}
4. Többen kimondták a következő sejtést: a nem konvex

n

-szögekre vonatkozó hasonló problémára is igenlő a válasz, ha nem metszik át önmaguk kerületét. A megnyugtató bizonyítás azonban nehéz lenne. A fentiekben megfordíthatónak tekintettük a ,,tapasz‐eljárást'', de nem konvex sokszögnél akár sok‐sok ide‐oda kanyarodás is lehetséges, áttekinthetetlen a sok lehetőség (9. ábra); maradjunk annál, hogy ez sejtés. (Vö. a sík lefedését egy bizonyos fajta nemkonvex

9

-szög egybevágó példányaival, Gy. 1898.^{$^{*}$})

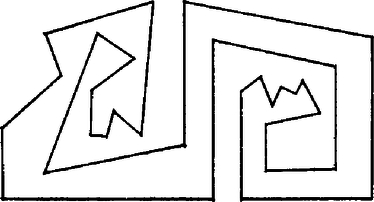9. ábra

5. Felbontható egy háromszög úgy is, hogy két oldalához fekete, egyhez fehér háromszög csatlakozzék (10. ábra). Ilyen elemekből is összerakható az

n

-szög felbontása.

10. ábra

^{$^{*}$}K.M.L. 1174. gyakorlat, 37 (1968), 12. o.

^{$^{*}$}1326. gyakorlat. K.M.L. 42 (1971) 166. o.

^{$^{*}$}Lásd a megoldást: Hajós György: Az 1967. év Kürschák József matematikai tanulóverseny feladatainak megodása, K.M.L. 36 (1968) 193 ‐ 202. oldal. A kapcsolódó megjegyzésekben többféle kiegészítés olvasható a tételhez.

^{$^{*}$}K.M.L. 61 (1980) 147-149. oldal és borítólap.