Kezdőlap


Feladat:	F.2282	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ákosfai Z. , Bali J. , Balla L. , Bán L. , Böröczky K. , Csere K. , Csillik Mária , Czimmer Aranka , Danyi P. , Eckert P. , Erdős L. , Feledi Gy. , Fodor Orsolya , Gerencsér Gy. , Halász P. , Hetyei G. , Holbok I. , Horváth A. , Horváth P. , Kánnai Z. , Kapos L. , Károlyi Gy. , Kerényi I. , Király Z. , Kis Urbán K. , Kozák P. , Ködöböcz Klára , Lados P. , Maloveczky Gy. , Megyesi G. , Méry Z. , Mihálykó Cs. , Mohay T. , Papp G. , Poór I. , Regős Enikő , Simek R. , Somogyi H. , Svidró Z. , Száraz S. , Szeredi Andrea , Szöllősi Gy. , Terenyi Z. , Törőcsik J. , Zauer G.
Füzet:	1981/október, 58 - 61. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Feladat, Síkgeometriai szerkesztések
Hivatkozás(ok):	Feladatok: 1980/november: F.2282

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mivel az $A'$ , $B'$ , $C'$ pontok adott helyzete csak az adott $P$ pontból feléjük futó félegyenesek kijelölésére szolgál, jelöléseink egyszerűsítése kedvéért feltesszük, hogy a keresett forgatás az $A$ , $B$ , $C$ pontokat rendre az $A'$ , $B'$ , $C'$ pontokba viszi.
A feladat két részre vágható: egyik rész az $A B C$ -vel egybevágó $A' B' C'$ háromszög megtalálása, a másik az előbbit az utóbbiba vivő forgatás előállítása. Az első részben elegendő az $A B C$ -hez hasonló háromszöget keresni, hiszen ha ilyet találunk, azt alkalmas méretű, $P$ centrumú nagyítás már a kívánt méretre transzformálja. Csak arra kell ügyelnünk, hogy az $A' B' C'$ háromszög $α, β, γ$ szögei forgásuk irányában is megegyezzenek az $A B C$ háromszög $α, β, γ$ szögeivel, hiszen a sík forgatásai a forgásszögek irányát nem változtatják meg.
A megoldás első lépéseként ezt a feladatot fordítjuk meg, és az $A$ , $B$ , $C$ csúcsokhoz olyan $P'$ pontot keresünk, amelyre a $P' A$ , $P' B$ , $' P C$ félegyeneseket ugyanolyan nagyságú és irányú forgatás viszi egymásba, mint a $P A'$ , $P B'$ , $P C'$ egyeneseket. Elegendő például azt biztosítani, hogy $P' A$ -t a $P' B$ -be ugyanakkora forgatás vigye, mint $P A'$ -t $P B'$ -be, és $P' B$ -t a $P' C$ -be ugyanakkora forgatás vigye, mint $P B'$ -t $P C'$ -be, hiszen a $P' C$ -t $P' A$ -ba vivő forgatás akkor már biztosan megegyezik a $P C'$ -t $P A'$ -be vivő forgatással.
Mivel mindkét követelmény egy-egy jól ismert mértani helyet jelöl ki az $A B C$ háromszög síkjában (egy $A B$ feletti és egy $B C$ feletti körívet), a szerkesztés első lépése ezek megrajzolásából áll, és a feladat megoldhatósága azon múlik, metszi-e egymást ez a két körív (1. ábra).

1. ábra

Nézzük meg, mit mondhatunk általában az

A' B' C'

háromszög

α', β', γ'

szögeiről, ha az

A'

B'

C'

pontok egymástól függetlenül bejárják a számukra adott félegyeneseket. Három, egy pontból induló félegyenes vagy lefedi a síkot, vagy nem, ami pontosabban azt jelenti, hogy a félegyenesek egyenese vagy rendre elválasztja egymástól a másik két félegyenest, vagy nem.
Ha a három adott félegyenes lefedi a síkot, az

A' B' C'

háromszög körüljárását eleve meghatározzák, a feladat tehát csak akkor oldható meg, ha ez megegyezik az

A B C

háromszög körüljárásával. Mivel ekkor

P

A' B' C'

háromszög belső pontja, belőle az oldalak rendre nagyobb szög alatt látszanak, mint a megfelelő csúcsokból. Ilyenkor tehát a feladat csak akkor oldható meg, ha

\begin{matrix} A B C ∢ < A' P C' ∢, B C A ∢ < B' P A' ∢, C A B ∢ < C' P B' ∢ . \end{matrix}

(1)

Ha ez teljesül, akkor az

A B

feletti, az

A' P C'

szöghöz tartozó látókörívnek van az

A B C

háromszög belsejében levő darabja. Ezen mozgatva a

P'

pontot az

A C

oldaltól a

B C

oldalig kezdetben. az

A P' C ∢

, majd a

B P' C

szög lesz

180^{\circ}

-kal egyenlő. Van tehát közben

P'

-nek olyan helyzete, amikor ezek az előírt szögekkel egyenlőek (2. ábra).

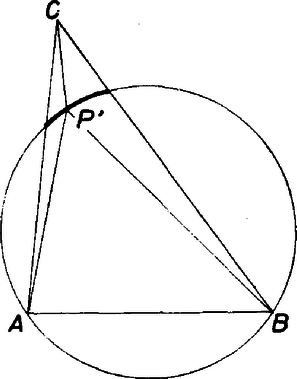2. ábra

Ha a három adott félegyenes nem fedi le a síkot, közülük csak az egyik egyenese választja el a másik két félegyenest, legyen mondjuk ez a

P C'

egyenes. Most nem határozzák meg a félegyenesek az

A' B' C'

háromszög körüljárását. Ha az

A' B'

egyenes elválasztja a

P

és

C'

pontokat, a félegyenesek és a háromszög körüljárása megegyezik, különben pedig fordított. Az utóbbi esetben

C'

lesz az

A' B' P

háromszög belső pontja, és a megoldhatóság feltétele

\begin{matrix} A' P B' ∢ < A' B' C' ∢, \end{matrix}

(2)

különben pedig az, hogy az

\begin{matrix} (A' P C' ∢ - A' B' C' ∢), (B' P C' ∢ - B' A' C' ∢) \end{matrix}

(3)

különbségek előjele megegyezzék, amint az a II. megoldásból könnyebben kiolvasható (3. ábra).

3. ábra

Ha már megtaláltuk azt a

P'

pontot, amelyre a

P' A

P' B

P' C

félegyenesek kölcsönös helyzete megegyezik a

P A'

P B'

P C'

egyenesekével, ezt tetszőleges olyan forgatás

P

-be viszi, amelynek az

O

centruma a

P P'

szakasz felezőmerőlegesén van. A forgatás nagyságát és irányát pedig megadja mondjuk a

P' A

P A'

félegyenesek közti szög.

O

helyét tehát egy újabb látókörív jelöli ki; ez a forgatás után a

P' B

P' C

félegyeneseket is a nekik megfelelő félegyenesekbe viszi, az

A B C

háromszöget pedig a keresett

A' B' C'

háromszögbe. Ha

P' A

és

P A'

párhuzamosak és egyirányúak, akkor forgatás helyett csak eltolásra van szükség, és persze előfordulhat, hogy

P

P'

azonosak.

II. megoldás (vázlat). Tovább egyszerűsítjük jelöléseinket, és elhagyjuk a vesszőket, hiszen a megoldást záró forgatás különösebb gondot nem okozhat. Felhasználjuk azt az I. megoldásban felbukkanó gondolatot is, hogy elegendő az adott háromszöghöz hasonlót találni, amelynek csúcsai már az adott félegyeneseken vannak. Adott tehát három félegyenes, és keressük rajtuk az

A

B

C

pontokat úgy, hogy az

A B C

háromszög szögei nagyságra és irányra megegyezzenek három adott szöggel. Legyen

A

B

C

P

az a pontnégyes, ami a megoldást jelenti.
Tekintsük azt az

A

centrumú forgatva nyújtást (vagyis

A

centrumú forgatást és ezt követő

A

centrumú nyújtást vagy zsugorítást), amelyik

B

-t

P

-be viszi. Vigye ez

C

-t

E

-be, és vigye

C

-t

F

-be az a

B

centrumú forgatva nyújtás, amelyik

A

-t viszi

P

-be. Belátható, hogy ekkor

\begin{matrix} \vec{P E} + \vec{P F} = \vec{P C} . \end{matrix}

(4)

Forgassuk el emiatt az adott

P A

félegyenest

P

körül akkora forgatással, ami a

B A

félegyenest

B C

-be viszi, és jelöljük a félegyenes új helyzetét

e

-vel. Majd forgassuk el

P B

-t

P

körül az

A B

-t

A C

-be vivő forgatással, így kapjuk az

f

félegyenest. Legyen

C

a számára adott félegyenes tetszés szerinti pontja. Bontsuk a

\vec{P C}

vektort

e

és

f

irányú komponensekre. Így kapjuk az

E

F

pontokat, amelyekbe a

C

-nél adott szöget behelyezve az

A

-t és

B

-t kimetsző félegyeneseket kapunk (4. ábra).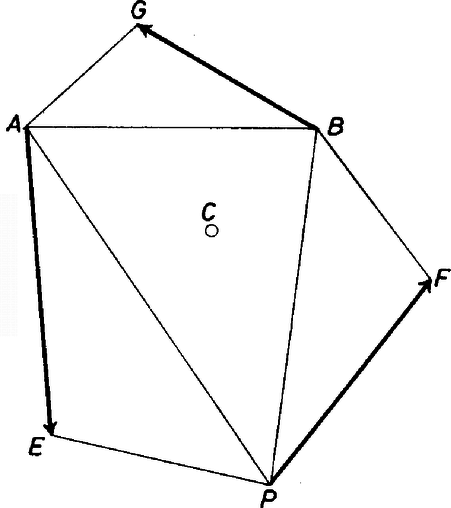

4. ábra

A feladat megoldhatósága tehát a (4) felbontáson múlik, amihez az kell, hogy az

e

f

félegyenesek fogják közre a

P C

félegyenest. Az olvasóra hagyjuk annak végiggondolását, hogy ebből valóban az (1), (2), (3) feltételeket kapjuk.

Megjegyzések. 1. A II. megoldásból látszik, hogy feladatunk azonos az úgynevezett ,,hátrametszéssel''. A térképészetben szerepel különösen gyakran az a feladat, hogy az ismeretlen helyzetű

P

pontot úgy azonosítjuk a síkon, hogy megmérjük, mekkora szögek alatt látszanak belőle az ismert

A

B

C

tereppontok. Lapunkban utoljára annak vizsgálata szerepelt ezzel kapcsolatban, hogy milyen mértékben csökken a módszer megbízhatósága, ha

P

-vel közeledünk az

A B C

háromszög köré írható körhöz. Ha ugyanis

P

ezen a ,,veszélyes'' körön van (aminek a (3) alatti különbségek eltűnése felel meg), akkor nem határozza meg, a helyzetét a

P A

P B

P C

félegyenesek kölcsönös helyzete.
2. Legyen még

C

-nek

A B

felezőpontjára vonatkozó tükörképe

G

, és jelöljük (tetszőleges origó mellett) a szóban forgó pontok helyvektorát a megfelelő kisbetűvel. Azt kell belátni, hogy (4. ábra)

\begin{matrix} e+f=c+p, \end{matrix}

és mivel

a + b = c + g

, ez azt jelenti, hogy

\begin{matrix} e+f+g=a+b+p, \end{matrix}

vagyis az

e - a, f - p, g - b

vektorok háromszöggé fűzhetők össze. Hát persze, az

A E C

háromszöggé, hiszen az

P A

-t

A E

-be,

P B

-t

P F

-be,

B A

-t

B G

-be vivő forgatva nyújtásokban a forgatás és a nyújtás azonos, csak a centrum más. Ha az

A B P

háromszög mindhárom oldalára ezt a transzformációt az

A

centrum mellett alkalmazzuk, akkor kapjuk az

A E C

háromszöget.