Kezdőlap


Feladat:	F.2275	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1981/március, 107 - 109. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1980/október: F.2275

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a keresett $A B C$ háromszög átfogója $A B$ , az $A$ -ból induló (belső) szögfelezőnek a $B C$ befogóval való metszéspontja $D$ . A beírt kör $O$ középpontját az $A D$ szakaszból az $A C D$ derékszög felezője metszi ki, és a $C O$ szakasz hossza $ϱ \sqrt[]{2}$ , ahol $ϱ$ a beírt kör előírt sugara. ‐ Ezek szerint feladatunkat lényegében megoldjuk, ha találunk eljárást az $A D C$ háromszög megszerkesztésére az $A D = f$ és e $ϱ \sqrt[]{2}$ hosszúságadatokból és a $C$ -beli $90^{\circ}$ -os szögből. Megjegyezzük, hogy $D A C ∢ < 45^{\circ}$ , ezért $D C < A C$ .
Az $A D$ szakasz fölötti $k$ Thalész‐kört a $C O$ szakasz meghosszabbítása az $A D$ -re merőleges átmérő $E$ végpontjában metszi, így lesz $D C E ∢ = E C A ∢ = = 45^{\circ}$ . Ekkor $A E O$ és $C E A$ hasonló háromszögek (2‐2 szögük páronként egyenlő), ennélfogva

\begin{matrix} A E : E O = C E : E A, \end{matrix}

(1)

amiből

\begin{matrix} E O \cdot E C = (E C - O C) E C = E C^{2} - C O \cdot E C = E A^{2} (= \frac{D A^{2}}{2}) . \end{matrix}

(1a)

Ezzel tulajdonképpen másodfokú egyismeretlenes egyenletet kaptunk

E C

-re, hiszen

E A

k

révén ismertté váló szakasz.

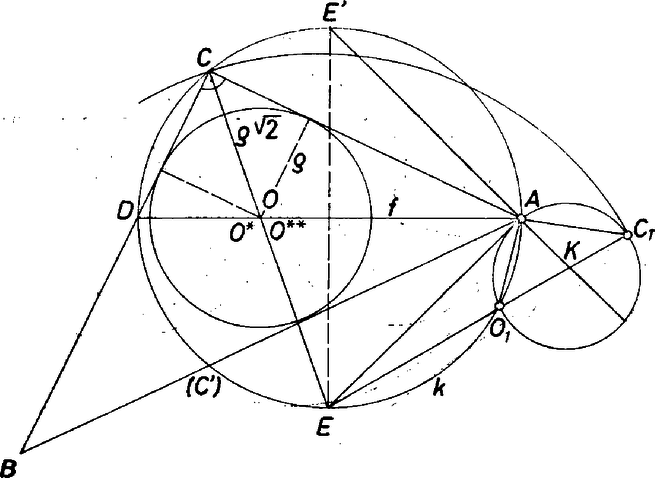Szerkesszük meg az

E A

egyenest

A

-ban érintő,

C O = ϱ \sqrt[]{2}

átmérőjü segédkört, jelöljük a középpontját

K

-val, továbbá az

E K

egyenesnek á segédkörrel való metszéspontjait

O_{1}

-gyel,

C_{1}

-gyel úgy, hogy

E C_{1} > E O_{1}

. Ekkor az

E A O_{1}

és

E C_{1} A

háromszögek hasonlók, hiszen

E

-ben közös szögük van és

E A O_{1} ∢ = E C_{1} A ∢

, ezért

\begin{matrix} E A : E O_{1} = E C_{1} : E A, \\ E O_{1} \cdot E C_{1} = (E C_{1} - C O) \cdot E C_{1} = E C_{1}^{2} - C O \cdot E C_{1} = E A^{2}, & (2) \end{matrix}

tehát

E C_{1}

eleget tesz

(1 a)

-nak. Hozzátesszük, hogy

E C_{1}

az egyetlen pozitív (vagyis számunkra használható) megoldás, mert

(1 a)

-t 0-ra redukálva az ismeretlent nem tartalmazó tag negatív:

- E A^{2}

, míg

E C^{2}

együtthatója

+ 1

. [És persze már az (1) felállításakor is pozitívnak gondoltuk a szereplő szakaszokat.]
Ezek alapján a szerkesztés, mindjárt teljesítve a feladat követelését is: az

E

körüli

E C_{1}

sugarú körrel kimetsszük

k

-ból

C

-t ‐ úgy, hogy

C A > C D

legyen ‐, vesszük

C

-nek

A D

-re való

C

tükörképét, ekkor a

C D

A C

egyenesek metszéspontja megadja a keresett háromszög hátra levő

B

csúcsát.
A kapott

A B C

háromszögben

C

-nél valóban derékszög van, benne

A D

felezi a

C A B

szöget, és beírt körének középpontja az

A D

és

C E

szögfelezők

O^{*}

metszéspontja. Azt kell még belátnunk, hogy a

C O^{*}

szakasz egyenlő az előírt

C O = C_{1} O_{1}

szakasszal. Mérjük fel

C E

-re a

C O^{* *} = C O

szakaszt. Ekkor a

C

O^{* *}

E

A

pontalakzatban

C E = C_{1} E

miatt teljesül (2) és (1a), tehát az (1)-nek megfelelő

A E : E O^{* *} = C E : C A

is, ezért

A E O^{* *}

és

C E A

hasonló háromszögek,

O^{* *} A E ∢ = A C E ∢ = 45^{\circ} = D A E ∢

, így

O^{* *}

D A

egyenesen van; másrészt

O^{* *}

C E

-n van, tehát azonos

O^{*}

-gal. Ennélfogva

C O^{*} = C O = ϱ \sqrt[]{2}

, tehát

O^{*}

-nak a

C B

és

C A

, továbbá az

A B

oldalaktól való távolsága valóban

ϱ

.
A

C

pont akkor és csak akkor jön létre a kör

D E'

negyedívén mint belső pont, ha

\begin{matrix} E D < E C < E E' = D A, \end{matrix}

amiből az első egyenlőtlenség nyilvánvalóan teljesül. A másodikhoz szükséges:

\begin{matrix} E K = E C - \frac{C O}{2} < D A - \frac{C O}{2}, \end{matrix}

amiből egyszerű számítással (minden pozitív)

\begin{matrix} \frac{f^{2}}{2} < f^{2} - f \cdot C O, C O = ϱ \sqrt[]{2} < \frac{f}{2}, f > \sqrt[]{8} ϱ . \end{matrix}

II. megoldás. Jelöljük (mint az I. megoldásban) az adott szakaszokat

ϱ

-val,

f

-fel, az

f

által felezett hegyesszöget

α

-val. A beírt kör középpontja a háromszög befogóival együtt egy

ϱ

oldalú négyzetet határoz meg, amelyhez két, egymással hasonló derékszögű háromszög csatlakozik. Ezek átfogóinak az összege

f

, egyik hegyesszögük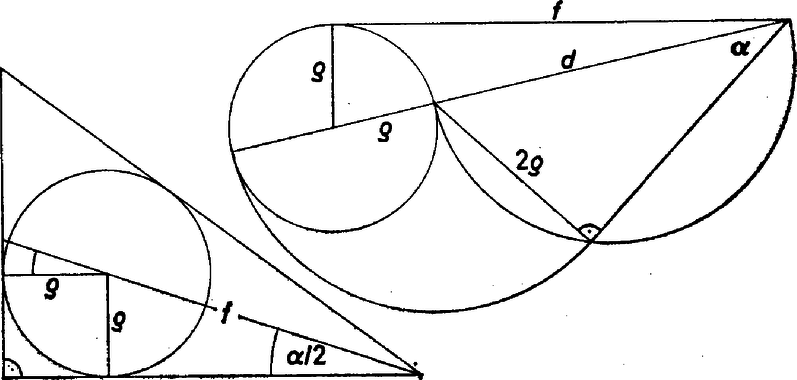

α / 2

, emiatt

\begin{matrix} \frac{1}{sin \frac{α}{2}} + \frac{1}{cos \frac{α}{2}} = \frac{f}{ϱ} . \end{matrix}

Jelöljük a jobb oldalon álló hányadost

λ

-val, és vegyük mindkét oldal négyzetét:

\begin{matrix} \frac{4 (1 + sin α)}{sin^{2} α} = λ^{2}, \end{matrix}

amiből teljes négyzetté kiegészítve kapjuk, hogy

\begin{matrix} {(\frac{2}{sin α} + 1)}^{2} = λ^{2} + 1. \end{matrix}

(1)

Mivel esetünkben

0 < sin α < 1

, a feladatnak csak akkor van megoldása, ha a jobb oldal értéke nagyobb 9-nél, vagyis

f > ϱ \sqrt[]{8}

. Ha ez teljesül, a kapott (1) összefüggés

α

értékét egyértelműen meghatározza. A szerkesztés kedvéért írjuk vissza

λ

értékét, kapjuk, hogy

\begin{matrix} {(d + ϱ)}^{2} = f^{2} + ϱ^{2}, \end{matrix}

(2)

ahol

d

annak a derékszögű háromszögnek az átfogója, amelynek az

α

-val szemközti befogója

2 ϱ

. Tehát az

f

ϱ

befogójú derékszögű háromszög átfogójából elveszünk egy

ϱ

-nyi darabot, majd a maradék fölé Thalész‐kört rajzolunk, és ezt a szakasz egyik végpontja körüli,

2 ϱ

sugarú körrel elmetszve megkapjuk az

α

szöget. Ebből és

ϱ

-ból a keresett háromszög már könnyen megrajzolható. Mivel a kapott (2) összefüggés ebben is érvényes, benne az

α

szög felezője egyenlő az adott

f

szakasszal, hiszen (2) ennek az értékét is egyértelműen meghatározza.