Kezdőlap


Feladat:	F.2262	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Csere K. , Kiss Ernő , Kiss György , Sz. Nagy Csaba , Szegedy P. , Takáts L. , Weisz F.
Füzet:	1980/november, 133 - 136. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletek, Vektorok, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1980/május: F.2262

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen egy, a föltevés szerinti $A B C$ háromszög magasságpontja $M$ , körülírt $k$ körének középpontja $O$ , és sugara a hosszúságegység, $A B$ oldalának felezőpontja $F$ , és ezekkel

\begin{matrix} M O = 2 \cdot F O . \end{matrix}

(1)

Vizsgálatunkat annak a szerkesztésnek a szemléletére alapítjuk, amellyel egy, a

k

-n belül megválasztott

F

-ből megkapjuk a háromszög csúcsait.

A

-t és

B

-t az

O F

-re

F

-ben állított merőleges metszi ki. Legyen

O

és

M

tükörképe

A B

-re

O^{*}

, ill.

M^{*}

, ismeretes, hogy

M^{*}

k

-n keletkezik. Így

O

M

M^{*}

és

O^{*}

egy szimmetrikus trapéz csúcsai, és (1) felhasználásával

\begin{matrix} O^{*} M^{*} = O M = 2 \cdot F O = O O^{*} . \end{matrix}

Ennélfogva

M^{*}

-ot az

O^{*}

közepű,

O

-n átmenő

k^{*}

kör metszi ki

k

-ból, és az

M^{*}

-on át

A B

-re állított merőlegesnek

k

-val való második metszéspontja

C

M^{*}

létrejön, ha az

O

O^{*}

M^{*}

pontokra teljesül

O O^{*} + O^{*} M^{*} \geq O M^{*}

, azaz

4 O F \geq 1

, tehát ha

O F \geq 1 / 4

. A szimmetria alapján elég azt az

M^{*}

-ot vennünk, amelyikre

M^{*} A \leq M^{*} B

; erre

C A \leq C B

is teljesül, és a szögek szokásos jelölésével

β \leq α

lesz. Ezért a vizsgálandó legnagyobbik szög

α

vagy

γ

.
Legyen

D

k

rögzített pontja,

F_{0}

O D

sugár negyedelő pontja:

O F_{0} =

= O D / 4

, és fussa be

F

F_{0} D

szakaszt; így

O^{*}

G H

szakaszt futja be, ahol

G

O D

felezőpontja és

H

O

tükörképe

D

-re.

D F_{0} \geq D F > 0

mellett minden vizsgálandó háromszöget megkapunk (viszont elfajulna a háromszög, ha

D

-ben vennénk fel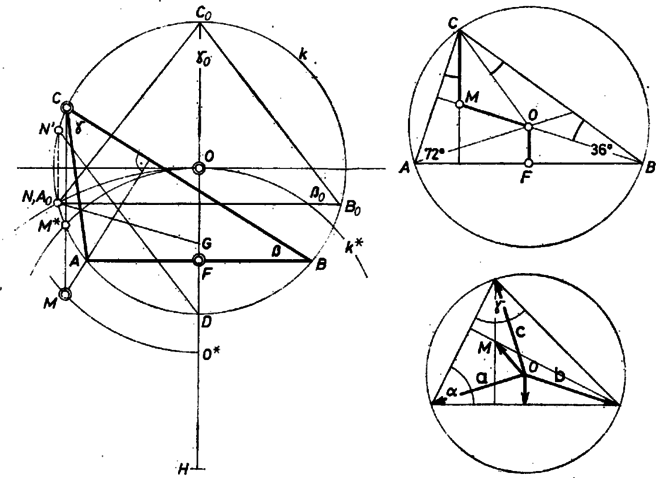

F

-et).

1‐3. ábra

F_{0}

-ból előálló

A_{0} B_{0} C_{0}

háromszög szimmetrikus az

O D

tengelyre ‐ hiszen ekkor

M^{*} = D

‐ és

\begin{matrix} tg \frac{γ_{0}}{2} = \frac{F_{0} A_{0}}{C_{0} F_{0}} = \frac{\sqrt[]{15}}{5} = \sqrt[]{0, 6}, cos γ_{0} = \frac{1}{4}, \end{matrix}

innen

γ_{0} = 75, 522^{\circ}

és

α_{0} = 90^{\circ} - γ_{0} / 2 = 52, 239^{\circ}

; itt tehát

γ_{0}

a legnagyobb szög.
Amint

F

halad

D

felé,

A

ugyancsak

D

felé közeledik a körvonalon,

M^{*}

viszont távolodik

D

-től, mert a

D O M^{*} ∢ = O^{*} O M^{*} ∢

nő, hiszen az

O^{*} M^{*} O

háromszög szárai, a

k^{*}

sugarai nőnek,

O M^{*}

alapja pedig változatlanul 1 egység. Továbbá

C

távolodik

C_{0}

-tól, hiszen

C

és

M^{*}

egymás tükörképei az

O D

-re merőleges átmérőre mint tengelyre. ‐ Ezek szerint

α

növekszik, mert

A B

iránya állandó,

γ

viszont a

D A

ív csökkenésével csökken, hiszen

γ = 2 \cdot D C A ∢

Könnyű látni, hogy az

A C

egyenes akkor lépi át az

O D

-vel párhuzamos helyzetet, amikor

F

G

-ben,

O^{*}

D

-ben van, és ezért

A

és

M^{*}

egybeesnek. Ekkor már

α = 90^{\circ}

a legnagyobbik szög (és

γ = 60^{\circ}

) és ez is marad.
Amint minden határon túl csökkentjük a

D F

távolságot, az

A

csúcs a

D

határhelyzethez közeledik,

O^{*}

H

-hoz,

M^{*}

ahhoz az

N

ponthoz, amelyet a

H

körüli

O

-n átmenő kör metsz ki

k

-ból, végül

C

N

tükörképéhez,

N'

-höz. Mármost

N

éppen

A_{0}

-ban adódik, mert az

N H O

egyenlő szárú háromszög oldalai rendre 2-szer akkorák, mint az

O A_{0} G

háromszögéi, az

O

közös csúcsuknál levő szögeik egyenlők, továbbá

O D

közös oldalegyenesük, ezért az

O N

O A_{0}

félegyenesek azonosak.
Ezek szerint

α

-nak felső korlátja a következő érték:

90^{\circ} + O D N' ∢ = 90^{\circ} + O C_{0} A_{0} ∢ = 90^{\circ} + \frac{γ_{0}}{2} = 127, 761^{\circ} ...

, és ezt

α

alulról tetszőleges kis eltéréssel megközelítheti.
Most már csak a legnagyobbik szög legkisebb értékét kell meghatároznunk. Kézenfekvő ez a sejtés: akkor adódik ez, amikor egyenlőnek adódik a csökkenőben levő

γ

és a növekedőben levő

α

.
Egy szerencsés ötlettel megpróbáltuk a fönti

γ_{0}

és a

γ = 60^{\circ}

közti

γ = 72^{\circ}

-ot. Megmutatjuk, hogy az

α = γ = 72^{\circ}

és

β = 36^{\circ}

szögekkel bíró (sok érdekességről ismert) háromszögben teljesül (1).
Minden háromszögben érvényes a

C M = 2 \cdot O F

összefüggés ‐ legutóbb a mostanival rokon F. 2221-ben láttuk ezt, az 1980. évi áprilisi számban (K. M. L. 60. kötet, 148. oldal), ennélfogva elég azt belátni, hogy a mondott szögek esetében

M O = M C

(2. ábra). Valóban,

M C A ∢ = 18^{\circ}

O C B ∢ = O B C ∢ =

= 18^{\circ}

, innen

M C O ∢ = 36^{\circ}

, másrészt

M O C ∢ = 1 / 2 A O C ∢ = A B C ∢ = 36^{\circ}

, tehát az

O C M

háromszög egyenlő szárú.
Mivel így a

72^{\circ}

-os közös érték átlépésekor fordul ellentétesre

α

és

γ

nagyságviszonya, ezért az (1) tulajdonságú háromszögekben a legnagyobbik szög pontos alsó korlátja

72^{\circ}

. Ezzel befejeztük kérdésünk vizsgálatát.

II. megoldás. Jelöljük a háromszög köré írt kör

O

középpontjából a csúcsokba mutató vektorokat a, b, c-vel úgy, hogy c mutasson abba a csúcsba, amellyel szemben fekvő oldal felezőpontjától vizsgáljuk

O

távolságát (3. ábra). Ez a távolság

\frac{1}{2} \cdot | a + b |

, mert

| a | = | b |

.
Ismert, hogy az

O

-ból az

M

magasságpontba mutató vektor

a + b + c

(Euler-egyenes), tehát

O M = | a + b + c |

. Ezek szerint a feltétel így írható:

\begin{matrix} | a + b | = | a + b + c | . \end{matrix}

Négyzetre emeléssel,

{| x |}^{2} = {(x)}^{2}

alapján

\begin{matrix} 0 = c^{2} + 2 a \cdot c + 2 b \cdot c \\ 0 = r^{2} + 2 r^{2} cos 2 β + 2 r^{2} cos 2 α, \end{matrix}

ahol

r

a körülírt kör sugara, a az

α

, b a

β

, c a

γ

szög csúcsához mutat, és a-t, b-t úgy választottuk meg, hogy a

α \geq β

. Átrendezéssel az eredeti feltétel

\begin{matrix} - \frac{1}{2} = cos 2 α + cos 2 β, \end{matrix}

és ez így is írható

\begin{matrix} \frac{1}{4} = cos (α - β) cos γ, \end{matrix}

(2)

ugyanis

\begin{matrix} cos x + cos y = 2 cos \frac{x + y}{2} cos \frac{x - y}{2} \end{matrix}

és

cos (180^{\circ} - x) = - cos x

, és

α + β + γ = 180^{\circ}

Jelölésünk szerint a legnagyobb szög

α

és

γ

valamelyike, mindenesetre nagyobb, mint

60^{\circ}

, hiszen szabályos háromszögben nem teljesül a feladat feltétele.
Nem lehet

γ

tompaszög, mert akkor vele együtt

(α - β)

is tompaszög lenne, hiszen (2) szerint cosinusaik egyező előjelűek. Így

\begin{matrix} \frac{1}{4} \leq cos γ < 1, 75, 522^{\circ} \geq γ > 0^{\circ} \end{matrix}

(

cos γ = 1

-ből elfajult háromszög adódnék). Minden ilyen érték megoldást ad az

\begin{matrix} α - β = arc cos \frac{1}{4 cos γ}, \\ α + β = π - γ \end{matrix}

egyenletrendszer szerint, innen

\begin{matrix} α = \frac{π}{2} - \frac{γ}{2} + \frac{1}{2} arc cos \frac{1}{4 cos γ}, \end{matrix}

(3)

és

γ = 0^{\circ}

mellett felső korlátot kapunk

α

-ra:

\begin{matrix} α < \frac{π}{2} + \frac{1}{2} arc cos \frac{1}{4}, \end{matrix}

és ez fokban

127, 761^{\circ}

Mivel

cos x

folytonos függvény és az inverze is az, a jobb oldali értéket

α

tetszőleges hibahatáron belül megközelítheti, a jobb oldali érték tehát

α

felső határa.
Másrészt

cos γ = 1 / 4

mellett

α = β = 52, 239^{\circ}

, ekkor

γ

a legnagyobb szög, vagyis a feladat feltételében kiemelt szerepű szög.
Azt is látjuk (3)-ból, hogy

γ

csökkenésével

α

nő, mert a kivonandó csökken, a hozzáadandó növekszik, ‐ és fordítva. Eszerint abban az esetben lesz minimális a legnagyobb szög értéke, ha

α = γ

. Keressük ezt a közös értéket! Írjunk (2)-ben mindkettő helyére

(90^{\circ} - \frac{β}{2})

-t:

\begin{matrix} \frac{1}{4} = sin \frac{3 β}{2} sin \frac{β}{2} = 3 sin^{2} \frac{β}{2} - 4 sin^{4} \frac{β}{2}, \\ sin^{2} \frac{β}{2} = \frac{6 \pm 2 \sqrt[]{5}}{16} = {(\frac{\sqrt[]{5} \pm 1}{4})}^{2}, \end{matrix}

tehát

β = 36^{\circ}

(a másik értékkel

β

tompaszög lenne) és

α = γ = 72^{\circ}

. Ebből az alakból elmozdulva vagy

α

növekszik, vagy

γ

, tehát a legnagyobb szög legkisebb értéke pontosan

72^{\circ}

Összegezve: a háromszög legnagyobb szöge

\frac{2 π}{5}

és

\frac{π}{2} + \frac{1}{2} arc cos \frac{1}{4}

(azaz

72^{\circ}

és

127, 76^{\circ}

) között minden értéket fölvehet, az alsó határt beleértve, a felső határt nem.

Megjegyzések. 1. Több olyan háromszög‐alaknak is megvan a vizsgált tulajdonsága, amelynek a szögei ún. "nevezetes'' szögek:

120^{\circ}

45^{\circ}

γ = 15^{\circ}

;

108^{\circ}

36^{\circ}

36^{\circ}

;

90^{\circ}

60^{\circ}

30^{\circ}

(itt van

β

minimuma):

γ = 75^{\circ}

60^{\circ}

45^{\circ}

2. A szögeket azért írtuk kétféle (fok, illetve radián) egységben, mert "arc cos''

x

‐ és minden arcus‐függvény ‐ ívmértékben értendő. A latin arcus szó éppen ívet jelent "árkuspapír''.

3. Természetesen vektorok nélkül is eljuthatunk (2)-re, például az 1980. áprilisi számunk 150. oldalán, az F. 2221. feladat megjegyzésében kimondott

\begin{matrix} {(\frac{O M}{r})}^{2} = {\begin{matrix} 4 (cos^{2} α + cos^{2} β + cos^{2} γ) - 3, \\ 9 - 4 (sin^{2} α + sin^{2} β + sin^{2} γ), \\ 1 - 8 cos α cos β cos γ \end{matrix} \end{matrix}

összefüggés és

O F = r cos γ

alapján. Itt mutatunk rá, hogy az idézett helyen a második kifejezés 4-es tényezője hiányzik.