Feladat: F.2255 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bohus G. ,  Dósa Gy. ,  Heckenast L. ,  Sz. Nagy Cs. ,  Szegedi P. 
Füzet: 1980/október, 67 - 69. oldal  PDF  |  MathML 
Témakör(ök): Logikai feladatok, Teljes indukció módszere, Feladat
Hivatkozás(ok):Feladatok: 1980/április: F.2255

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A bizonyítást teljes indukcióval végezzük. n=1 esetben 0 a szükséges kérdések száma, hiszen egy tudós biztosan piripócsi.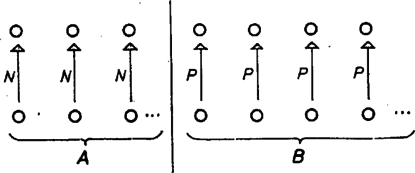
Tegyük fel, hogy k tudós származását megtudhatjuk k2/2 kérdéssel. Megmutatjuk, hogy ekkor k+1 tudóst megismerhetünk (k+1)2/2 kérdéssel.
Válasszunk ki egy tudóst, T-t és kérdezzük meg a többieket, hogy T honnan jött. Mivel a tudósok többsége piripócsi, a többségben levő válaszok megadják, hogy T hova való. Ha egyik válasz sincs többségben, tehát k/2 tudós állítja, hogy T piripócsi és k/2, hogy nekeresdi, akkor a kérdezett tudósok fele hazudik, így T csak piripócsi lehet.
A továbbiakban két esetet vizsgálunk. Ha T piripócsi, tőle újabb k-1 kérdéssel megtudhatjuk a többi tudós származását, így 2k-1<(k+1)2/2 kérdés elég.
Ha T nekeresdi, őt kihagyjuk a társaságból. A piripócsiak többségben maradnak, így ezt a k tudósból álló társaságot az indukciós feltevés szerint megismerhetjük k2/2 kérdéssel. Így összesen legfeljebb k22+k=(k+1)2-12 kérdést használtunk fel, tehát az állítás igaz.
Természetesen ezt a módszert tovább lehet finomítani, a kérdések száma csökkenthető, de hogy 10n kérdés is elég, azt egy másik algoritmus segítségével bizonyítjuk.
Az indukciós feltevésünk az, hogy ha egy k<n tagú társaságban a nekeresdiek száma kevesebb a piripócsiakénál, akkor legfeljebb 2k kérdéssel el tudjuk dönteni, ki honnan jött. n=1 esetében ez nyilván igaz.
Bebizonyítjuk, hogy ha a társaság n tagú, 2n kérdés elég. Tegyük fel először, hogy n páros. Állítsuk párba a tudósokat az ábra szerint, és kérdezzük meg az alsókat, honnan származik a felső sorban álló párjuk. Ezután osszuk a tudósokat két csoportra: az A csoportba tartozzanak azok a párok, ahol a válasz: Nekeresd, a B csoportba pedig azok, ahol a válasz: Piripócs. Az A csoportban legyen 2a, a B csoportban 2b tudós.

 
 

Az A-beli párokban legalább az egyik tudós nekeresdi, hiszen ha mindkettő piripócsi lenne, akkor bármelyikük a másikat piripócsinak mondaná. A-ban tehát a piripócsiak legfeljebb annyian vannak, mint a nekeresdiek, ezért a B csoport nem lehet üres és benne több piripócsinak kell lennie, mint nekeresdinek. Tovább menve azt is észrevehetjük, hogy ha B alsó sorában egy tudós piripócsi, akkor az ő felső párja is piripócsi, hiszen azt állítja róla. Ebből az következik, hogy B felső sorában álló b tudós közt több a piripócsi, mint a nekeresdi, így az indukciós feltevés szerint őket 2b kérdéssel megismerhetjük. Közülük egy piripócsitól már megtudhatjuk, hogy a többi 2a+b tudós honnan jött. A felhasznált kérdések számát megvizsgálva:
(a+b)+2b+(2a+b)=3a+4b≤4a+4b=2n,hiszen most2a+2b=n.

Ha n páratlan, akkor a párba állítás után marad egy tudós. Ha b páros, vegyük őt a B csoport felső sorához. Ha ott ugyanannyi piripócsi van, mint nekeresdi, akit kihagytunk, csak piripócsi lehet, tehát az új csoportban több a piripócsi, mint a nekeresdi. Ha pedig B felső sorában eleve több a piripócsi, mint a nekeresdi, akkor legalább 2-vel több, hiszen b páros, tehát bárhonnan jött is a kihagyott tudós, őt közéjük véve is megmarad a piripócsiak többsége. Ha azonban b páratlan, nem szabad a kihagyott tudóst a B felső sorában állók közé venni. Szerencsére nincs is erre szükség, hiszen most ott biztosan több piripócsi van, mint nekeresdi. Az eljárás és a bizonyítás mindkét esetben ugyanígy fejezhető be, mint páros n-re.
 
 Szegedy Patrik (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)
 

Megjegyzések. 1. Sokan estek abba a hibába, hogy a megoldás első felében használt gondolatmenet alapján nemleges választ adtak a feladat második kérdésére.
2. Nem ismert, hogy mennyi a legkevesebb kérdés, amennyivel még biztosan célhoz lehet érni. Nyilvánvalóan legalább n/2 kérdést fel kell tennünk (mindenkiről valamilyen információt kell szereznünk, és egy kérdéssel két tudósról tudunk meg valamit). Ruzsa Imre igazolta, hogy 5n/4 kérdésre feltétlenül szükség van. Ismeretes olyan taktika, amely 3n/2 kérdés után eldönti, hogy ki hová való.
3. Az a feltétel, hogy a piripócsiak többen legyenek, feltétlenül szükséges. Ha például m piripócsi és m nekeresdi volna a kongresszuson, továbbá a nekeresdiek egymást piripócsinak, a piripócsiakat nekeresdinek mondanák, nem lehetne eldönteni, hogy ki hová való.