| Feladat: | F.2254 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Füzet: | 1980/november, 126. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Két pont távolsága, szakasz hosszúsága, Mértani helyek, Feladat, Vektorok | ||
| Hivatkozás(ok): | Feladatok: 1980/április: F.2254 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A kenguru (, ) pontból (, ) pontba való ugrását nevezzük kis ugrásnak, a másikat nagy ugrásnak. 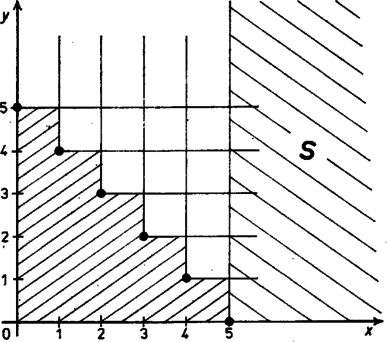 Vizsgáljuk meg, az első síknegyednek melyek azok a pontjai, amelyekből a kenguru nem juthat el az negyedsíkba. Mivel az első síknegyed -en kívüli pontjaiból a kenguru nem tud nagyot ugrani, csak kis ugrások segítségével kerülhet -be. Fordítsuk meg a kenguru útját! Az negyedsíkot eltolva rendre a (, 1), 2(, 1), , 5(, 1) vektorokkal, megkapjuk mindazon pontok mértani helyét, melyekből a kenguru eljuthat -be. Állítjuk, hogy az első síknegyedből kimaradó lépcsős alakzat adja a feladat megoldását. Azt, hogy egy ebbe nem eső pontból a kenguru tetszőlegesen messze eljuthat az origóból, éppen most láttuk be. Másrészt a "lépcső'' pontjaiból a kenguru nagyot ugrani nem tud (mert akkor kikerülne az első síknegyedből), ha pedig kicsit ugrik, továbbra is a lépcső egy pontjába jut. Ezzel a feladat kérdését megválaszoltuk. Könnyen látható, hogy a "lépcső'' pontjait az , , egyenlőtlenségrendszer határozza meg. |