Kezdőlap


Feladat:	F.2232	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1980/április, 153 - 154. oldal		PDF \| MathML
Témakör(ök):	Szinusztétel alkalmazása, Feladat, Trigonometriai azonosságok
Hivatkozás(ok):	Feladatok: 1979/december: F.2232

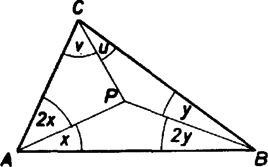
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $P$ az $A B C$ háromszögben mondjuk az $A$ -beli és $B$ -beli szögharmadolók metszéspontja:

\begin{matrix} x = P A B ∢ = \frac{1}{3} C A B ∢; y = P B C ∢ = \frac{1}{3} A B C ∢ . \end{matrix}

P A B

P B C

P C A

háromszögekben a szinusztétel alapján

\begin{matrix} P B : P A = sin x : sin 2 y, P C : P B = sin y : sin u, P A : P C = sin v : sin 2 x, \end{matrix}

ahol

u

P C B

v

P C A

szöget jelöli. Mivel e három arány szorzata 1,

\begin{matrix} sin x sin y sin v = sin 2 y sin u sin 2 x, \end{matrix}

vagyis

\begin{matrix} \frac{sin v}{sin u} = 4 cos x cos y, \end{matrix}

(1)

hiszen

sin 2 x = 2 sin x cos x

sin 2 y = 2 sin y cos y

. Mivel

cos x cos y = cos (x + y) + sin x sin y > cos (x + y)

, és itt

(x + y)

kisebb

60^{\circ}

-nál, emiatt (1) jobb oldalának az értéke nagyobb 2-nél:

\begin{matrix} \frac{sin v}{sin u} > 2, \end{matrix}

(2)

így sem

u

, sem

v

nem lehet a

B C A

szög harmada.

Csak formálisan jelent új lehetőséget a

P A B ∢ = \frac{1}{3} C A B ∢

eset mellé a

P B A ∢ = \frac{1}{3} C B A ∢

esetet felvenni, hiszen ekkor

P C B ∢ = \frac{1}{3} A C B ∢

esetén

B

és

C

P C A ∢ = \frac{1}{3} B C A ∢

szög esetén pedig

C

és

A

léphet a fenti meggondolásba

A

és

B

helyére. Ezzel beláttuk, hogy nincs olyan

A B C

háromszög, amelynek a belsejében volna olyan

P

pont, hogy az

A P

B P

C P

félegyenes rendre harmadolja a

B A C

C B A

A C B

szöget.