Kezdőlap


Feladat:	F.2228	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Rátz Ákos
Füzet:	1980/március, 115 - 116. oldal		PDF \| MathML
Témakör(ök):	Súlyvonal, Körülírt kör középpontja, Két pont távolsága, szakasz hosszúsága, Feladat
Hivatkozás(ok):	Feladatok: 1979/november: F.2228

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a $B C$ oldal felezőpontját $F$ -fel. Amíg $O$ , $F$ és $P$ egymástól különbözők (és $A$ -tól is), az $O P A$ és $O P F$ (valódi) derékszögű háromszögekből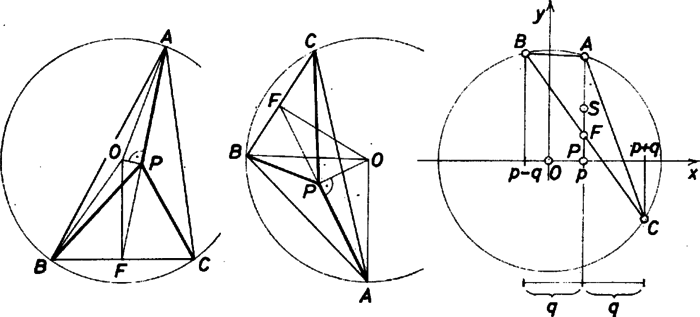

\begin{matrix} P A^{2} = 0 A^{2} - O P^{2} = O B^{2} - (O F^{2} - P F^{2}) = B F^{2} + P F^{2} = \frac{B C^{2}}{4} + P F^{2}, \end{matrix}

hiszen

O A = O B

. Vegyük észre, hogy itt

P F

P B C

háromszög

P

-ből induló súlyvonala, tehát ismert összefüggés szerint

\begin{matrix} P F^{2} = \frac{1}{4} (2 P B^{2} + 2 P C^{2} - B C^{2}), \end{matrix}

ezt beírva

\begin{matrix} P A^{2} = \frac{1}{2} (P B^{2} + P C^{2}), \end{matrix}

szavakban:

P A

négyzetes közepe a

P B

P C

hosszúságoknak.

A fönt egyelőre kizárt esetekben is érvényes a talált összefüggés, de semmitmondó.

P

azonos

O

-val, ha

A F

egyenes átmegy

O

-n, és ekkor a háromszög egyenlő szárú:

A B = A C

, a vizsgált

3

hosszúság egyenlő. És akkor is ez áll, ha mindjárt

F

azonos

O

-val, vagyis a kiindulási háromszögben

A

-nál derékszög van. (

F

és

P

egybeesése lehetetlen az

O

-tól különböző pontban.)

Megjegyzés. A súlyvonalra felhasznált kifejezés bizonyítható abból, hogy paralelogramma oldalainak négyzetösszege egyenlő az átlók négyzetösszegével; ez pedig a Pitagorasz-tételnek az átlókra mint átfogókra való alkalmazásából, a befogók irányainak az egyik oldalpárt és a hozzájuk tartozó magasságot véve. (Kiadódik a cosinustétel alkalmazásával is, de az kerülő út.)

II. megoldás. Helyezzünk derékszögű koordináta-rendszert alakzatunkra, origóját tegyük a kör

O

középpontjába, ordinátatengelyét pedig állítsuk párhuzamosra az

A F

súlyvonallal. Ez azt jelenti, hogy

A

és

F

abszcisszája közös, jelöljük

p

-vel, így

P

koordinátái (

p

0

B

és

C

abszcisszái pedig

p - q

p + q

alakúak, és körünk sugarát hosszúságegységnek választva ordinátáik is kifejezhetők. (Csak a négyzetükre lesz szükségünk.)

\begin{matrix} P A^{2} & = 1 - p^{2}, \\ P B^{2} & = q^{2} + (1 - {(p - q)}^{2}) = 1 + 2 p q - p^{2}, \\ P C^{2} & = q^{2} + (1 - {(p + q)}^{2}) = 1 - 2 p q - p^{2} . \end{matrix}

Vegyük észre, hogy innen

\begin{matrix} 2 p q = P B^{2} - P A^{2} = P A^{2} - P C^{2}, \end{matrix}

tehát

\begin{matrix} P B^{2} + P C^{2} = 2 \cdot {P A}^{2} . \end{matrix}

Rátz Ákos (Győr, Révai M. Gimn., IV. o. t.)