Feladat: F.2227 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Balázsi Ildikó ,  Beleznay F. ,  Csere K. ,  Feledi Gy. ,  Fodor L. ,  Horváth I. ,  Kappelmayer Hedvig ,  Kelemen B. ,  Kirchner I. ,  Kiss E. (Győr) ,  Kiss Gy. (Miskolc) ,  Kovács I. (Eger) ,  Pongrácz A. ,  Simonyi G. ,  Szegedy P. ,  Takáts L. (Sopron) ,  Umann G. 
Füzet: 1980/május, 202 - 206. oldal  PDF  |  MathML 
Témakör(ök): Térfogat, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat, Egyéb poliéderek
Hivatkozás(ok):Feladatok: 1979/november: F.2227

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A test lapjainak az a) követelményre tekintettel 3 vagy 4 vagy 5 oldaluk van. A d) előírás szemben fekvő oldalakról szól a c) szerinti lappal szomszédos lapokon ‐ vagyis legalább 3 lapon ‐, ezeken tehát páros, azaz 4 az oldalak száma. De akkor van további négyszöglap is, mert síklapokkal határolt testen a páratlan oldalszámú lapok száma páros ‐ ami itt már csak 2 vagy 0 lehet. Valóban, lapról lapra összeadva az oldalak számát, az összeg az élek számának 2-szerese, páros szám, ezért a páratlan összeadandók száma páros.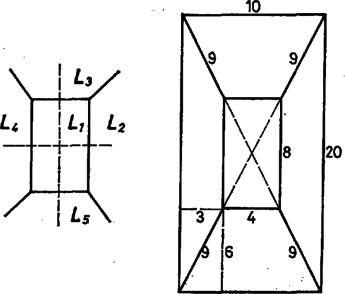
Az S1 és S2 szimmetriasíkok merőlegesen állnak egymásra. Így ugyanis mindegyiknek a másikra való tükörképe önmaga, különben pedig ‐ akár párhuzamosak volnának, akár hegyes szöget zárnának be egymással ‐ S1-nek S2-re való tükörképe, az S1* sík új, meg nem engedett szimmetriasík lenne (lásd a megjegyzést). Legyen S1 és S2 metszésvonala t.
Önmagába megy át a test akkor is, ha előbb S1-re, majd S2-re tükrözzük; az eredmény az, mintha elforgatjuk t mint tengely körül 180∘-kal.
Ezek szerint a test egy csúcsának, élének, lapjának általában 3 tőle különböző képe van, a tükrösen rokon elemek 4-esével felelnek meg egymásnak. Ha azonban egy csúcs vagy él benne van Si-ben, ha egy él vagy lap merőleges Si-re (i=1 vagy 2), akkor ennek az elemnek arra a síkra való képe maga az illető elem, így csak a másik síkra való képe különböző tőle. Ha pedig a t-n van rajta egy csúcs, illetve ha a t-re merőleges egy él vagy egy lap síkja, ennek az elemnek nincs önmagától különböző képe. (Él nem lehet t-ben a konvexség miatt.)

 

 
1. ábra

 

Nevezzük az ilyen szimmetrikus együtteseket röviden klikkeknek. (A szó hétköznapi jelentéséhez képest némi hasonlóság mutatkozik elemeik összetartozásában és mások kizárásában.) Esetünkben tehát a test minden egyes csúcsa, éle, lapja a szimmetria szempontjából vagy egy 4- vagy egy 2- vagy pedig egy 1-elemű klikkbe tartozik bele. Speciális esetek: 2-elemű lapklikk elemeiből a ,,másik'' Si sík szimmetriatengelyt metsz ki; hasonlóan a t-re merőleges lapnak két szimmetriatengelye és szimmetriacentruma van.
Szeleteljük végig a testet a t-re merőleges M síkokkal, a leírt szimmetriák e metszetekben is megmutatkoznak. (A tengelyt függőlegesnek tekintjük.)
 

I. Vegyük elsőnek azt az esetet, ha M-nek mindjárt az ,,első kontaktusában'' (meginduló helyzetében) egy L1 lapot kapunk M és a test közös részeként. Ez kéttengelyű idom, tehát négyszög, oldalai mentén csatlakoznak az L2-L5 lapok.
1. Ha L1 téglalap ‐ vagyis csúcsai 4-elemű klikket alkotnak, élei pedig két 2-elemű klikket ‐, akkor az utóbbiak révén L2-L5 is két 2-elemű lapklikket alkot, az L1 csúcsaiból induló harmadik élek pedig 4-elemű élklikket (1. ábra). (További él nem indulhat L1 csúcsaiból, mert 1‐1 ilyen további 4 lapot jelentene.) Így az utolsó lap, L6 klikkje ismét 1-elemű, ezért merőlegesen áll t-re, tehát ez is négyszög és párhuzamosan áll L1-gyel. Eszerint L2-L5 síkjai párhuzamos élekben metszik L2 és L6 síkját, az L2-L5 lapok trapézok, L6 pedig szintén téglalap.
Mindez csak úgy egyeztethető össze a méretkövetelményekkel, hogy a c) és e) lapok L1, és L6, a d)-lapok pedig szimmetrikus trapézok, száraik 9 egységnyiek; a test csonkagúlaszerű.
Valóban csonkagúlát kapunk a 10:20=4:8 egyenlőség alapján, ha a két téglalap hosszú oldalai állnak párhuzamos párokban, mert ekkor a trapézszárak meghosszabbításai t-ben metszik egymást. Az alapokra való vetületük hossza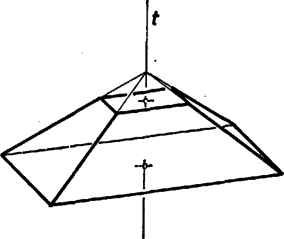
(20-82)2+(10-42)2=45,
a párhuzamos lapok távolsága 81-45=6 egység, a térfogat az ismert képlet szerint 624 térfogategység (2. ábra).
 

 
2. ábra

 

Ha a 4×8-as kis alapot úgy állítjuk, hogy 4-es oldala a nagy alap 20-as oldalával legyen párhuzamos, akkor a párhuzamos lapok távolsága hasonló számítással 4 egység. Két-két szomszédos oldalél páronként metszi egymást, de már hármuknak sincs közös pontjuk. A 4×8-as alap élein átmenő (függőleges) síkokkal 9 részre darabolva a testet, közülük 1 téglatest lesz, 4 rész gúla, egybevágók, alapjuk téglalap (ez is egy klikk), és 4 rész az oldallapján fekvő 3 oldalú hasáb (páronként egybevágók, alaplapjaik derékszögű háromszögek). E részek összegeként a térfogat 4422/3 egység, kisebb az előbbinél (3. ábra).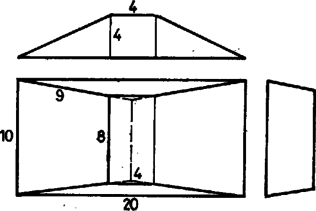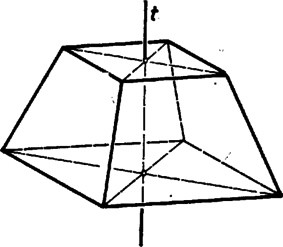
 

 
3. ábra

 

 
4. ábra

 

2. Lényegében ugyanígy kapjuk, hogy a szimmetriakövetelményt az olyan 6 lapú testek is teljesítik, amelyeknek L1 és L6 lapja rombusz, L2-L5 lapjai egy klikket alkotnak; az ilyen testeken azonban legföljebb 4 különböző élméret fordulhat elő (ezek is csonkagúlák, 4. ábra).
 

II. Milyen testek jönnek szóba, ha M első kontaktusában egy e1 élt kapunk ? Ez 1-elemű klikk, legyen a rajta átmenő szimmetriasík S1; végpontjai 2-elemű klikket alkotnak, a belőlük induló 2‐2 él, valamint másik végpontjaik 4-eleműt (5a ábra). Negyedik él nem futhat ki e1 végpontjaiból, mert az ilyenek S1-ben lennének, az S1 két oldalán 3‐3 lapú testek jönnének létre csupa háromszöglapokkal. A kettős 3 oldalú szabályos gúlát az is kizárja, hogy 3+1 szimmetriasíkja van (6. ábra). További, 5-élű stb. válfajok elképzelésének is a lapok 6-os száma szab korlátot.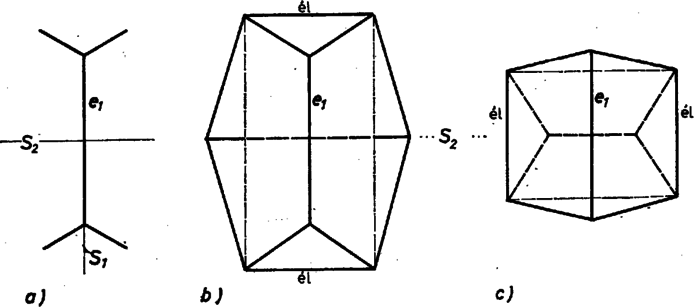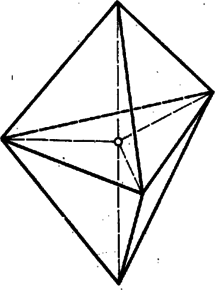
 

 
5. ábra

 

 
6. ábra

 

Nem lehet, hogy az 5a. ábra 4 ,,befejezetlen'' csúcsa egy lapban legyen, vagyis az általuk meghatározott téglalap mindegyik oldala él legyen, mert így 5 lapunk lenne csak; de az sem, hogy a velük meghatározott téglalap egyik oldala sem él ‐ hanem csupán lapbeli átló ‐, mert emígy az eddig megkezdett 4 lapot ismét nem lehetne 2 lappal befejezni. (Gondolja át az olvasó !) Ha viszont két oldalt tekintünk élnek a téglalapból, ennek mindkét befejezése lehetséges (a további csúcsok S2-ben). Feladatunkban azonban nem felelnek meg, mert négyszöglapból csak 2 van rajtuk (5b és c ábra, M utolsó metszete is él, a 2 eredmény lényegében azonos).
 

III. Nem felel meg olyan test sem, amilyet abból a kiindulásból kapunk, hogy a metsző sík kiinduló M1 helyzetében csak egy C csúcsot tartalmaz a testből ‐ de ez ismét csak az élméreteken múlik. Ismét kettéválik vizsgálatunk az M1 ,,utáni'' metszetek téglalap, ill. rombusz volta szerint ‐ így C mindenképpen 4-élű csúcs.
1. Tekintsük az első olyan téglalap-metszetet, amelyben van további csúcsa a testnek. Ez 4-elemű klikkbe tartozik, és ennek a téglalapnak ismét csak 2 szemben levő oldala lehet él. Ezek 2 egyenlő szárú háromszöget zárnak le, tovább pedig 4 négyszöglap adódik, ebből 2 tengelyszimmetrikus trapéz, 2 deltoid (esetleg rombusz). A 10 és 20 élméreteket a háromszögekre téve, egyikük megismétlődik a deltoidok 2 szomszédos oldalán, tehát azokon nem helyezhető el két 9 egységnyi élhossz; a négyszöglapok közül pedig egyiket sem csupa páros oldalszámú lap veszi körül (7. ábra).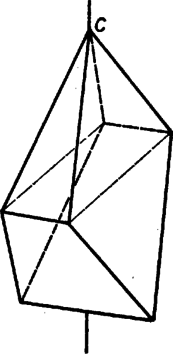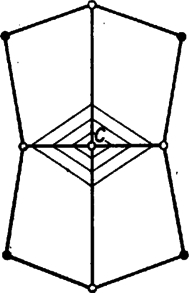
 

 
7. ábra
 

 
8. ábra

 
Az M1 utáni rombusz-metszetek esetében a C-ből kifutó élek az Si-kben vannak, C-ben 4 elemű lapklikk fut össze. Emiatt csak négyszögekről lehet szó, az Si-ken kívüli 8 befejezetlen élükhöz való csatlakozásra ismét kevés a 2 hátra levő lap (8. ábra).
Minden szóba jött testtípust számba vettünk és közben a legnagyobb térfogatú testet is megadtuk.
 

Megjegyzések. 1. A szimmetriasíkok merőleges állását elég belátni a t-re merőleges síkon kimetszett t1,t2 és t1* szimmetriatengelyeken. Valóban, tükrözve egy P0 pontot, valamint t1-re való P01 képét a t2-re, a keletkező P02 és P012 képek különbözők és egymásnak is képei a t1*-re nézve (9. ábra).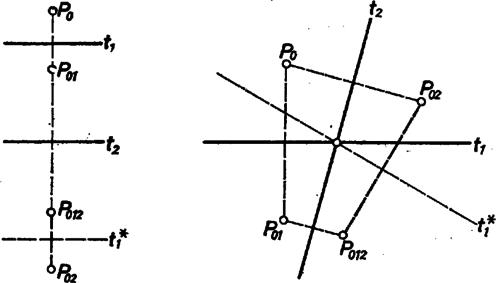
 

 
9. ábra

 
2. A különböző típusú (ún. topológiailag különböző) konvex 6-lapú testek száma 7, ezek különböző típusú lapjainak, csúcsainak számát, szimmetriasíkjainak, tengelyeinek legföljebb lehetséges számát az alábbi táblázat mutatja.
Az ebben az értelemben egymástól különböző konvex 7-lapok típusainak száma már több, mint 30; ott az ilyen létszámok már nem is elegendőek a típusok megkülönböztetésére.
 


 Lapok  Csúcsok  Szimmetria   4 oldalú   3 oldalú   5 oldalú    3 élű      4 élű      5 élű   sík   forgás-     tengely6‐‐8‐‐9    13       (kocka)  4    2  ‐  6    1    ‐    2     1  2    2    2    8    ‐    ‐    2     1  2    3    1    6    1    ‐    1     ‐  2    4    ‐    4    2    ‐  ‐     1  ‐    5    1    5    ‐    1    5     1  ‐    6    ‐    2    3    ‐    4     4