Kezdőlap


Feladat:	F.2221	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Benkó B. , Berkes L. , Csizmadia Bernadett , Czakó F. , Fodor L. , Gabura G. , Gregor Z. , Halász P. , Horváth 718 I. , Juhász I. , Kainráth Éva , Kappelmayer Hedvig , Keszei Zs. , Kis 963 Gyöngyi , Kocsis G. , Kunsági M. S. , Maloveczky Gy. , Mészáros G. , Mihálykó Cs. , Sárközi Ágnes , Sárvári G. , Sz. Nagy Cs. , Szabó 457 L. , Szakál Tünde , Tóth G. , Umann G.
Füzet:	1980/április, 148 - 151. oldal		PDF \| MathML
Témakör(ök):	Koszinusztétel alkalmazása, Vektorok, Feladat
Hivatkozás(ok):	Feladatok: 1979/október: F.2221

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mivel $O A = 1$ , azért $cos M O A ∢$ "hossza'' az $O A'$ szakasz előjellel vett hosszát jelenti, ahol $A'$ az $A$ csúcs vetülete az $O M$ egyenesen, a pozitív irányt $O$ -tól $M$ felé választva. Így azt kell belátnunk, hogy hasonló jelölésekkel

\begin{matrix} O A' + O B' + O C' = O M . \end{matrix}

(1)

Megjegyezzük, hogy szabályos háromszögben

M

egybeesik

O

-val ‐ és semmilyen más háromszögben nem ‐, ott nincs értelme az állításnak.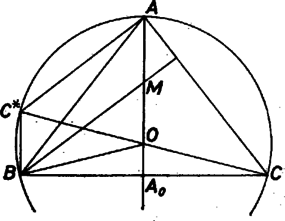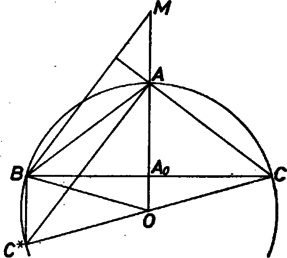

1. ábra

2. ábra

Célszerű az egyenlő szárú háromszögeket is külön elintézni, ilyenekben az

O M

egyenes maga a szimmetriatengely. Legyen

A B = A C (\neq B C)

, a kör

C

-vel átellenes pontja

C^{*}

, és a

B C

oldal felezőpontja

A_{0}

; így

B'

és

C'

egybeesik

A_{0}

-lal,

A'

pedig

A

-val, tehát mindjárt

O A' = O A

. Az

M A C^{*} B

négyszög paralelogramma ‐ ez az

A B \neq A C

esetben is igaz ‐, mert 2‐2 oldala merőleges

C B

-re, illetve

C A

-ra, ezért ‐ az irányt most is beleértve ‐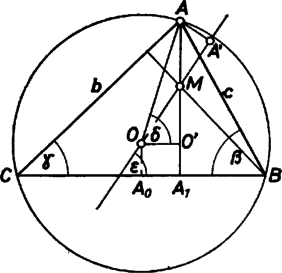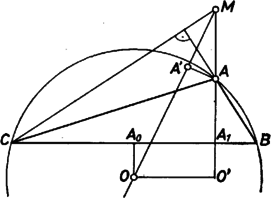

\begin{matrix} M A = B C^{*} = 2 A_{0} O = - 2 O A_{0} = - (O B' + O C'), \end{matrix}

és ezekkel (1) bal oldala így alakul

\begin{matrix} O A' + (O B' + O C') = O A - M A = O M, \end{matrix}

és ezt akartuk megmutatni (1. és 2. ábra)

3. ábra

4. ábra

Az általános esetre térve, a 3. és 4. ábrán úgy választottuk a betűzést, hogy teljesült az

A C = b > c = A B

nagyságviszony, tehát

β > γ

is. Legyen

A

vetülete

B C

-re

A_{1}

, és

O

vetülete

A A_{1}

-re

O'

. Az

M O A

látószöget az

O A

O M

egyenesek

C B

-hez való

δ

ε

hajlásszögeinek különbségeként határozzuk meg. Az elsőre

\begin{matrix} δ = 90^{\circ} - O A A_{1} ∢ = 90^{\circ} - (C A A_{1} ∢ - C A O ∢) = \\ = γ + \frac{180^{\circ} - C O A ∢}{2} = 90^{\circ} - (β - γ) . \end{matrix}

A másikra, mindjárt a föntebbiek felhasználásával és átalakításokkal, ismert azonosságok alapján

\begin{matrix} cos ε = \frac{O O'}{O M} = \frac{cos δ}{O M} = \frac{sin (β - γ)}{O M}, és \\ sin ε = \frac{O' M}{O M}, \end{matrix}

ahol

\begin{matrix} O' M = A_{1} A - A_{1} 0' - M A = c sin β - 3 A_{0} O = 2 sin γ sin β - 3 cos α = \\ = cos (β - γ) - cos (β + γ) + 3 cos (β + γ) . & (2) \end{matrix}

Ezekkel

\begin{matrix} O A' = O A cos (δ - ε) = \frac{1}{O M} (sin^{2} (β - γ) + cos^{2} (β - γ) + 2 cos (β - γ) cos (β + γ)) = \\ = \frac{1}{O M} (1 + cos 2 β + cos 2 γ) . \end{matrix}

Mondjuk ki ehhez mindjárt:

O A'

"érzéketlen'' a bevezetett

β > γ

nagyságviszonyra, tehát megfelelő betűcserékkel hasonló kifejezést írhatunk fel

O B'

-re és

O C'

-re.
Ezekkel a bizonyítandó (1) a következő alakot veszi föl:

\begin{matrix} 3 + 2 (cos 2 α + cos 2 β + cos 2 γ) = O M^{2} = O' O^{2} + O' M^{2} . \end{matrix}

(3)

Itt a jobb oldal a (2) és

O' O = sin (β - γ)

alapján, valamint a legutóbbi alakításokat megismételve

\begin{matrix} sin^{2} (β - γ) + cos^{2} (β - γ) + 4 cos (β - γ) cos (β + γ) + 4 cos^{2} α = \\ = 1 + (2 cos 2 β + 2 cos 2 γ) + (2 + 2 cos 2 α), \end{matrix}

vagyis egyenlő (3) bal oldalával. Ezzel az állÍtást minden háromszögre bebizonyítottuk, hacsak

M

nem azonos

O

-val.

Megjegyzés. A (3) bal oldalának alakításaival az

O M

távolságra az alábbi kifejezéseket is fölírhatjuk:

\begin{matrix} {(\frac{O M}{r})}^{2} = 4 \cdot \sum_{}^{3} cos^{2} α - 3 = 9 - \sum_{}^{3} sin^{2} α = 1 - 8 \prod_{}^{3} cos α, \end{matrix}

ahol

\sum^{3}

a 3 db

cos^{2} α

"típusú'' tag összegének kiírását rövidíti,

\prod^{3}

pedig a 3 db

cos α

"típusú'' tényező szorzatának kiírását; ilyenféle rövidítéseket inkább a fizikában szokás alkalmazni.

II. megoldás: Helyezzünk koordináta‐rendszert az ábránkra úgy, hogy az origója

O

legyen, és

M

x

tengely pozitív felére essék. Ebben a koordináta‐rendszerben az I. megoldásban használt (1) összefüggés azt jelenti, hogy az

\vec{O A}

\vec{O B}

\vec{O C}

vektorok első koordinátáinak összege egyenlő

\vec{O M}

első koordinátájával. Megmutatjuk, hogy ennél több is igaz, nevezetesen

\begin{matrix} \vec{O A} + \vec{O B} + \vec{O C} = \vec{O M} . \end{matrix}

(1*)

Helyezzük az

\vec{O A} + \vec{O B} + \vec{O C}

összeg kezdőpontját

O

-ba, és jelöljük ebben a helyzetben a végpontját

M^{*}

-gal. Ekko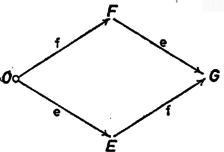r

\begin{matrix} \vec{O A} + \vec{O B} + \vec{O C} = \vec{O M^{*}}, \end{matrix}

így (1*) azt jelenti, hogy

M^{*}

azonos

M

-mel

5. ábra

Legyenek e és f tetszőleges irányú, egységnyi nagyságú vektorok, legyen

O

a közös kezdőpontjuk, a végpontjuk pedig

E

és

F

. Toljuk át

f

kezdőpontját

E

-be, új helyzetében a végpontja legyen

G

. Ekkor (5. ábra)

\begin{matrix} \vec{O G} = \vec{O E} + \vec{E G} = e + f, \end{matrix}

hiszen két vektor összeadásának egyik módja az, hogy egymás után fűzzük őket. Ugyanemiatt

\begin{matrix} \vec{E F} = \vec{O F} - \vec{O E} = e - f . \end{matrix}

Ha e és f azonosak,

\vec{E F}

az ún. null‐vektor. Ha e és f azonos állásúak, de ellentétes irányúak, akkor

\vec{O G} = 0

. Különben az

O

E

G

F

pontok paralelogrammát határoznak meg, és ebben

E F ⊥ O G

, tehát (e

+

f) merőleges (e

-

f)-re. Mondjuk azt a könnyebb beszéd kedvéért, hogy két vektor merőleges egymásra, ha állásaik merőlegesek, ha egyikük hossza sem nulla, vagy pedig valamelyikük (esetleg mindkettő) hossza 0. Így most már feltétel nélkül mondhatjuk, hogy (e

+

f) merőleges (e

-

f)-re. Mivel

\vec{O A}

\vec{O B}

egységnyi,

\vec{O A} + \vec{O B} = \vec{O M^{*}} - \vec{O C} = \vec{C M^{*}}

merőleges az

\vec{O A} - \vec{O B} = \vec{B A}

vektorra. Ugyancsak merőleges

\begin{matrix} \vec{O B} + \vec{O C} = \vec{A M^{*}} az \vec{O B} - \vec{O C} = \vec{C B} vektorra, és \\ \vec{O C} + \vec{O A} = \vec{B M^{*}} az \vec{O C} - \vec{O A} = \vec{A C} vektorra . \end{matrix}

Itt

\vec{B A}

\vec{C B}

\vec{A C}

hossza nem lehet 0, mert egy háromszög oldalvektorai. Ha

\vec{A M^{*}}

\vec{B M^{*}}

\vec{C M^{*}}

valamelyike 0, akkor abban a csúcsban van a háromszög magasságpontja, amelyikkel

M^{*}

azonos, hiszen ekkor

O

a szemközti oldal felezőpontja. Különben az

A M^{*}

és

A M

B M^{*}

és

B M

C M^{*}

és

C M

egyenesek azonosak, ami csak úgy lehet, ha

M^{*}

azonos

M

-mel.

Megjegyzések. 1. Egy sík vektorai között kétféleképp szokás szorzást definiálni; az egyik eredménye szám, azért ezt "skaláris'' szorzásnak hívják, a másik eredménye vektor, így ez a "vektoriális'' szorzás. Az a, b vektorok skaláris szorzata

| a | \cdot | b | cos ε

, ahol

ε

az a, b közti szög. (Ha a, b valamelyike 0, a szorzat 0.) A definícióból kiolvasható, hogy ez a szorzás kommutatív, így erre is érvényes az (a

+

b)(a

-

b)=a

^{2}

-b

^{2}

összefüggés. Ebből is látszik, hogy egységvektorok összege és különbsége merőleges egymásra.

2. Ismeretes, hogy

\begin{matrix} \vec{O S} = \frac{1}{3} (\vec{O A} + \vec{O B} + \vec{O C}), \end{matrix}

ahol

S

a háromszög súlypontja. Ezt (1*)-gal összevetve kapjuk, hogy

\vec{O M} = 3 \vec{O S}

, vagyis

S

O M

szakasz

O

-hoz közelebbi harmadolópontja. Feladatunk II. megoldása erre az (Eulertől származó) állításra szokásos bizonyítások egyikének adaptálása.