| Feladat: | F.2204 | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Füzet: | 1979/november, 135 - 136. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kombinatorikus geometria síkban, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1979/április: F.2204 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Miután megrajzoltuk egy konvex -szög néhány átlóját a kívánt módon, osztályozzuk a csúcsokat a belőlük induló átlók száma szerint. Fessük is be, mondjuk, sárgára azokat a csúcsokat, amelyekből csak egy átló indul, és barnára, amelyből több. Ha van barna csúcs, a belőle induló átlók legyezőszerűen szétterülnek, közülük a többiekhez viszonyított helyzetük alapján kettőt szélsőnek, a többit, ha van ilyen, belsőnek mondunk. Megmutatjuk, hogy egy barna csúcsból induló bármely belső átló másik végpontja csak sárga lehet. Az ilyen átló ugyanis úgy vágja ketté a síkot, hogy a barna végpontjából induló két szélső átló különböző félsíkokban. van. Emiatt azokat egyszerre egyetlen, a belső átló másik végpontjából induló szakasz sem metszheti. ‐ barna csúcsba csak a két szélső átló katonái mehetnek. 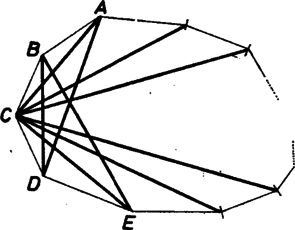 Végül megmutatjuk, hogy ha , akkor ez a felső korlát el is érhető. (Ha , akkor eleve nincs átlónk, így a korlát nyilván nem érhető el. Az és esetek azonban könnyen elintézhetőek, hiszen az elsőben nincs átló, a másodikban pedig két, egymást metsző átló van.) Legyen , , , , az -szög öt egymás utáni csúcsa. Rajzoljuk meg az , , , , átlókat, és ha , a -ből induló összes további átlót. A megrajzolt átlók közül ‐ a -ből indulóknak a közös végpontjuk, ‐ bármely -ből induló átló metszi az , , átlókat, hiszen bármely -ből induló átló egyenese elválasztja egymástól az ‐ , ‐ , ‐ párok tagjait, és mivel a sokszög konvex, a metszéspont csak az átlón keletkezhet; ‐ az , , illetve , átlóknak közös végpontjuk van, és pedig metszik egymást. A kérdezett szám tehát , ha , és különben. |