Feladat: F.2201 Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Arató M. ,  Balázs P. ,  Bölcsföldi L. ,  Csirke Zs. ,  Erdélyi T. ,  Fodor L. ,  Fordán T. ,  Gabriel Z. ,  Grolmusz V. ,  Kántor Zs. ,  Karacs F. ,  Kirchner I. ,  Kiss 352 Gy. ,  Kurusa Á. ,  Pátkai Andrea ,  Sz. Nagy Cs. ,  Szegedy P. ,  Tálas Cs. ,  Varga J. ,  Varga Lívia 
Füzet: 1979/november, 130 - 131. oldal  PDF  |  MathML 
Témakör(ök): Gráfelmélet, Kombinációk, Teljes indukció módszere, Feladat
Hivatkozás(ok):Feladatok: 1979/április: F.2201

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha a társaságnak van olyan tagja, aki legalább 4 másikat nem ismer, akkor ez utóbbiak közül bármely kettőnek ismernie kell egymást, azaz máris találtunk négy megfelelő embert. Így feltehetjük, hogy mindenkinek legalább 5 ismerőse van a szobában. De nem lehet mindenkinek pontosan 5 ismerőse, mert az 5⋅9/2 ismeretséget jelentene, ami pedig nem egész. Kell tehát lennie legalább 6 ismerőssel rendelkező embernek is, legyen A ilyen, A ismerősei közül pedig egyik legyen B.
Ha B az A ismerősei közül legalább hármat ismer, akkor ezek közül valamelyik kettő A-val és B-vel együtt megfelelő négyest alkot. Ha nem, akkor B az A ismerősei közül legalább hármat nem ismer, ez a három és A lesz a jó négyes.
Így tehát minden esetben találtunk olyan négyest, akik kölcsönösen ismerik egymást.

 
Megjegyzések. 1. Ez a feladat emlékeztet az F. 2187. feladatra, mindkettő a gráfelmélet egy-egy picike tételét tárgyalja.
2. Teljes indukcióval könnyen be lehet bizonyítani a következő tételt. Ha egy szobában n(n+1)/2 ember van és bármely három között van kettő, akik ismerik egymást, akkor van a szobában n ember, akik közül bármely kettő ismeri egymást. Jelöljük f(n)-nel azt a legkisebb egészt, amit n(n+1)/2 helyébe téve még mindig igaz marad az állítás. Könnyű ellenőrizni hogy f(2)=3, f(3)=6 és f(4)=9. A feladatban f(4)≤9-et bizonyítottuk, míg f(4)>8-at a mellékelt ábra mutatja.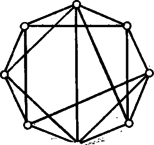
 
 

Az f(n) függvényről tudjuk, hogy vannak olyan c1 és c2 konstansok, melyekre
c1⋅n2(lgn)2<f(n)<c2⋅n2lgn
teljesül minden n-re. A bal oldali egyenlőtlenséget Erdős Pál, a jobb oldalit Szemerédi Endre bizonyította.