Kezdőlap


Feladat:	F.2197	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1979/szeptember, 15 - 16. oldal		PDF \| MathML
Témakör(ök):	Két pont távolsága, szakasz hosszúsága, Kör (és részhalmaza), mint mértani hely, Rombuszok, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1979/március: F.2197

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a rombusz átlóinak hosszát $2 e$ -vel, $2 f$ -fel, és válasszuk az átlók egyeneseit koordináta-rendszerünk tengelyeinek; így a rombusz csúcsainak koordinátái: 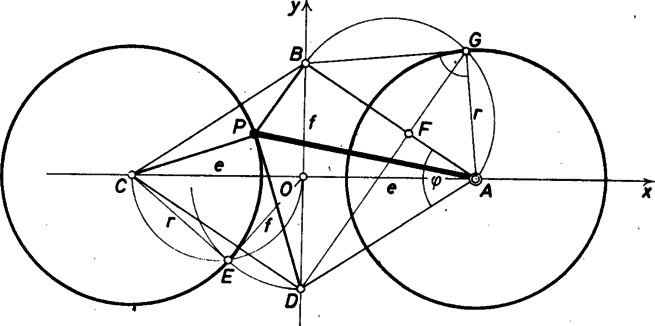$A$ ( $e$ , $0$ ), $B$ ( $0$ , $f$ ), $C$ ( $- e$ , $0$ ), $D$ ( $0$ , $- f$ ).

Adjuk a feladat szerinti kiemelt szerepet először az

A

csúcsnak, erre az esetre a mértani helynek mint

e

és

f

függvényének definícióját a következő egyenlet fejezi ki:

\begin{matrix} P A^{2} = P B^{2} + P C^{2} + P D^{2}, \end{matrix}

azaz

\begin{matrix} {(x - e)}^{2} + y^{2} = [x^{2} + {(y - f)}^{2}] + [{(x + e)}^{2} + y^{2}] + [x^{2} + {(x + f)}^{2}], \end{matrix}

ahol

P (x, y)

a ponthalmaz tetszőleges pontja. Innen rendezés útján és mindjárt teljes négyzetté kiegészítéssel

\begin{matrix} {(x + e)}^{2} + y^{2} = e^{2} - f^{2} . \end{matrix}

(1)

e^{2} - f^{2} > 0

, azaz

e > f (> 0)

esetében annak a körnek az egyenlete, melynek középpontja

C

(az

A

-val szemben fekvő csúcs) és sugara

r = \sqrt[]{e^{2} - f^{2}}

; ha

e = f

, akkor (1)-et csak a

C

pont elégíti ki, végül

0 < e < f

esetében semmilyen pont sem elégíti ki kapott egyenletünket, a keresett halmaz üres.
Rögzítsük most az

e > f

nagyságviszonyt, ekkor a feladat szerinti "valamelyik'' csúcs szerepét sorra

A

-nak,

B

-nek,

C

-nek,

D

-nek adva, az 1. és a 3. esetben egy-egy kört kapunk

C

, ill.

A

körül a fönti

r

sugárral, a 2. és 4. eset viszont nem hoz járulékot a halmazhoz, tehát a mértani hely az

A

és

C

pontok ‐ a rombusz hegyesszögű csúcsai ‐ körüli

r

sugarú körök egyesítése.
Ha viszont speciálisan

e = f

, akkor a követelményt a négyzetté specializálódott rombusznak a négy csúcsa elégíti ki, más pont nem.
Lépéseink megfordíthatók, tehát a két kör pontjai valóban megfelelnek.
Egyszerű eljárást adhatunk a körök megszerkesztésére: legyen az

O C

félátló fölötti Thalész-kör és az

O

körüli,

D

-n átmenő kör egyik közös pontja

E

, itt átmegy a

C

körüli kör (

e < f

esetén

E

nem jön létre).

Megjegyzés. Többen a rombusz egyik csúcsát vették origónak és az innen induló oldalak egyikét az egyik koordinátatengelynek. A számítás így kissé hosszabb, de az az érdekes eredmény adódik, hogy a két kör sugara

A B \sqrt[]{cos D A B ∢}

, a szög természetesen szükséges volt a további két csúcs paraméterének.
Kiadódik persze ez a fenti eredményből is

\begin{matrix} e = A B cos \frac{φ}{2}, f = A B sin \frac{φ}{2} \end{matrix}

és

\begin{matrix} e^{2} - f^{2} = A B^{2} (cos^{2} \frac{φ}{2} - sin^{2} \frac{φ}{2}) = A B^{2} cos φ . \end{matrix}

És még egy szerkesztést is kiolvashatunk belőle: ha

D

vetülete az

A B

oldalra

F

(és

A F < A B

), akkor

r = A G

A B

A F

szakaszpár mértani középarányosa, és

G

is pontja a mértani helynek.