Feladat: F.2196 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bacsi Zsuzsanna ,  Balázs P. ,  Beleznay F. ,  Bodócs P. ,  Bogdán Klára ,  Bohus G. ,  Bozsó P. ,  Buczolich Z. ,  Bukta Gy. ,  Csordás A. ,  Feledi Gy. ,  Fodor L. ,  Gaál I. ,  Gát Gy. ,  Golarits I. ,  Hajnal P. ,  Horváth 169 T. ,  Horváth Á. ,  Kántor Zs. ,  Kardos J. ,  Király E. ,  Kőrösi G. ,  Kőrösi Katalin ,  Kozák Ágnes ,  Lőrinczi Zsuzsanna ,  Márkus L. ,  Mikó Teréz ,  Pintér 395 F. ,  Ruisz T. ,  Soós Marianna ,  Sz. Nagy Cs. ,  Szalai Cs. ,  Szegedy P. ,  Tóth I. ,  Varga J. ,  Varga Lívia ,  Varga T. ,  Winkler R. ,  Öreg E. Zsolt 
Füzet: 1979/november, 127 - 129. oldal  PDF  |  MathML 
Témakör(ök): Derékszögű háromszögek geometriája, Szögfelező egyenes, Háromszögek szerkesztése, Alakzatok köré írt kör, Feladat
Hivatkozás(ok):Feladatok: 1979/március: F.2196

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az adott oldal végpontjait B, C-vel, hosszát a-val, a szemközti csúcsot A-val, a körülírt kört k-val, középpontját K-val, sugarát r-rel, BC felezőpontját E-vel, az A-beli szögfelező BC-vel és k-val való metszéspontját D-vel, ill. F-fel, k-nak F-fel átellenes pontját G-vel, az AD szakasz adott hosszát d-vel. Kezdjük a háromszög szerkesztését K és k felvételével, ezután a nyilvánvaló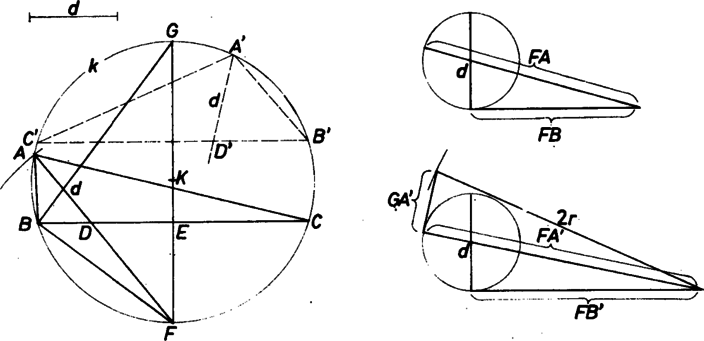

a≤2r
feltétel teljesülése esetén a BC húr és a rá merőleges FG átmérő is megrajzolható. (Ugyanis a szögfelezés miatt F felezi az BC ívet.)
 

 
1. ábra

 

Mivel az ADEG négyszögben A-nál és E-nél derékszög van, a négyszög köré kör írható. E körre nézve F külső pont (1. ábra)
FA⋅FD=FE⋅FG=FB2,(1)
és itt ismerjük az FA-FD=d különbséget. Az utolsó alakítás azon alapszik, hogy az FGB háromszög derékszögű.
Rajzoljunk hát valahol egy d átmérőjű kört, és ehhez FB-vel egyenlő hosszúságú érintő szakaszt. Ennek szabad végpontját a kör középpontjával összekötve kapjuk azt a szelőt, amelynek a darabjai FA-val, FD-vel egyenlőek (és persze FA>FD). A kapott FA szakasz természetesen csak akkor használható fel A kijelölésére, ha nem nagyobb 2r-nél (az alulról való FA>FB korlátozó követelmény nyilván mindig teljesül). Ezzel megkaptuk a háromszöget.
Mivel az A csúcs elvileg az ábra ,,alsó'' BC ívén is létrejöhet ‐ K-tól a BC által elválasztva ‐, azért a leírt szerkesztést úgy is meg kell kísérelnünk, hogy F szerepét G-nek adjuk át. (Az 1. ábrán azonban jobb áttekintés érdekében F-et rögzítettük és BC-nek B'C' tükörképéből ismételtük a szerkesztést.) Az ábrán fölvett d szakaszból mindkét esetben 2r-nél kisebbnek adódott FA.
 
Megjegyzések. 1. Eljuthatunk (1)-re hasonló háromszögpárok alapján is, ilyenek FBD és CAD, valamint FDE és FGA.
2. Elkerülhetjük segédábra használatát és megtakaríthatjuk az érintő szerkesztését, ha a főábra FB (ill. GC) szakaszához illesztjük a d átmérőjű kört úgy, hogy B legyen az érintési pont, vagyis a kör középpontja a GB (ill. FC) egyenesen legyen. Így az F-ből a kör középpontján át húzott egyenes által kimetszett A*, D* körpontok a körző tűhegyének fölemelése nélkül átfordíthatók A-ba, D-be. (A 2. ábra az előzővel egyenlő méretek mellett készült.)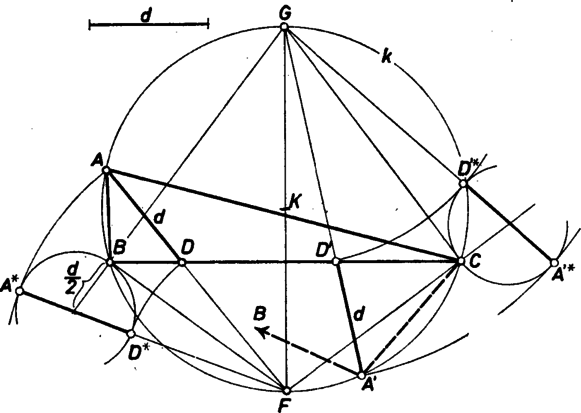
 

 
2. ábra

 

Ebben az ügyes elrendezésben végezve a szerkesztést, több helyen ,,klasszikusnak'' minősítik a megoldást. Ha még ezt is fölírjuk (1) alapján:
FA=d2+(d2)2+FB2,
akkor az érdeklődők bizonyára észreveszik a rokonságot a szabályos 5- és 10-szög oldalának, illetve egy szakasz aranymetszés szerinti kettéosztásának jól ismert Ptolemaiosz ‐ Dürer-féle szerkesztésével.
Többen rámutattak, hogy a feladat ,,félbehagyva'' szerepelt 1976. szeptemberi számunk 25. oldalán mint az Iskolarádió Szakkörének előkészítő anyaga. ‐ És persze ‐ mint ,,híres'' feladat ‐ szerepelt már előbb többször is, pl. az 1962. májusi szám 201. oldalán. (3 megoldásból 2 speciálisan derékszögű háromszögre vonatkozik az ottani kitűzés szerint.)
4. Ha a c oldal helyett a γ szög volna adott, elmaradna F és G megkülönböztetése.