Kezdőlap


Feladat:	F.2192	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1979/október, 64 - 66. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Csonkakúp, Terület, felszín, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1979/február: F.2192

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Válasszuk egységnek a gömb sugarát, és jelöljük a csonkakúpot határoló síkoknak a gömb középpontjától mért távolságát $x$ -szel, illetve $y$ -nal. Mivel a csonkakúpot félgömbbe írtuk, a középpont nem lehet a két sík között. Válasszuk úgy a betűzést, hogy $x < y$ teljesüljön, és legyen továbbá $x = sin α$ , $y = sin β$ . Akkor a csonkakúpot határoló körlapok sugara $cos α$ , $cos β$ , a palást alkotója $2 sin \frac{β - α}{2}$ , és a csonkakúp felszíne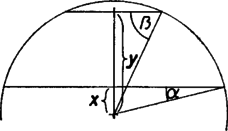

\begin{matrix} F = π [cos^{2} α + cos^{2} β + 2 (cos α + cos β) sin \frac{β - α}{2}] . \end{matrix}

Rögzített

β

mellett ez

α

-ban monoton fogy, tehát

α = 0

mellett maximális. Ezt behelyettesítve, és a kapott függvényt

β

szerint deriválva az

\begin{matrix} f (β) = - 2 cos β sin β - 2 sin β sin \frac{β}{2} + (1 + cos β) cos \frac{β}{2} \end{matrix}

függvényt kapjuk (a

π

konstanst elhagytuk). Ebből némi átalakítás után az

\begin{matrix} f (β) = 2 (4 sin^{3} \frac{β}{2} - 3 sin^{2} \frac{β}{2} - 2 sin \frac{β}{2} + 1) cos \frac{β}{2} \end{matrix}

alak adódik. Mivel itt a zárójelben álló kifejezés együtthatóinak összege 0, ebből

(sin \frac{β}{2} - 1)

kiemelhető:

\begin{matrix} f (β) = 2 (4 sin^{2} \frac{β}{2} + sin \frac{β}{2} - 1) (sin \frac{β}{2} - 1) cos \frac{β}{2} . \end{matrix}

A kapott másodfokú kifejezés gyökei

\frac{- 1 \pm \sqrt[]{17}}{8}

, közülük

sin \frac{β}{2} > 0

miatt csak

\begin{matrix} sin \frac{β}{2} = \frac{\sqrt[]{17} - 1}{8} \end{matrix}

jöhet szóba. Itt a másodfokú kifejezés előjele negatívból pozitívvá válik,

sin \frac{β}{2} < 1

cos \frac{β}{2} > 0

miatt

f (β)

értéke pedig éppen fordítva, pozitívból vált negatívba. Emiatt annak a függvénynek, amelyiknek

f (β)

a deriváltja, ezen a helyen maximuma van, és a szóba jöhető

0 < β < 90^{\circ}

értékek mellett ez az egyetlen szélsőérték. Tehát az egységnyi sugarú félgömbbe írható maximális felszínű csonkakúp egyik határolólapja azonos a félgömböt határoló körlappal, a másik attól

\begin{matrix} y = sin β = 2 sin \frac{β}{2} cos \frac{β}{2} = 0, 7188 \end{matrix}

távolságra van.

Megjegyzés. Megoldásunkban két fontos deriválási szabályt is felhasználtunk, amelyek a használatban levő függvénytáblázatban ugyan megtalálhatóak, de a tankönyvben nem. Az egyik szerint a sin függvény deriváltja a cos függvény, a másik szerint a deriválható

u

és

v

függvények szorzata is deriválható, és a derivált

(u' v + u v')

, ahol

u'

v'

szokás szerint

u

és

v

deriváltját jelöli. Mivel

\begin{matrix} sin α - sin β = 2 sin \frac{α - β}{2} cos \frac{α + β}{2}, \end{matrix}

és

{lim}_{x \to 0}^{} \frac{sin x}{x} = 1

, valóban igaz, hogy

\begin{matrix} {lim}_{ε \to 0}^{} \frac{sin (β + ε) - sin β}{ε} = {lim}_{ε \to 0}^{} \frac{sin \frac{ε}{2}}{\frac{ε}{2}} \cdot {lim}_{ε \to 0}^{} cos (β + \frac{ε}{2}) = cos β . \end{matrix}

A szorzatra vonatkozó állítás pedig a

\begin{matrix} {lim}_{ε \to 0}^{} \frac{u (x + ε) \cdot v (x + ε) - u (x) \cdot v (x)}{ε} = \\ = {lim}_{ε \to 0}^{} \frac{u (x + ε) - u (x)}{ε} v (x + ε) + {lim}_{ε \to 0}^{} u (x) \frac{v (x + ε) - v (x)}{ε} \end{matrix}

átalakítás segítségével igazolható.