Feladat: F.2190 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1979/október, 60 - 62. oldal  PDF  |  MathML 
Témakör(ök): Trigonometriai azonosságok, Függvény határértéke, Egyéb ponthalmazok a koordinátasíkon, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):Feladatok: 1979/február: F.2190

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A vizsgált háromszög benne van a C(r,p), D(p,p), E(p,r), F(r,r) csúcsok által meghatározott négyzetben, mégpedig A a DE, B pedig az EF oldalon helyezkedik el. Jelöljük még a (q,p), (r,q) koordinátájú pontokat A'-vel, B'-vel, ezek A, B-nek a négyzet DF átlójára vonatkozó tükörképei. Az AB'CD téglalapban B'AC∢=ACD∢, és mivel ez a téglalap egybevágó az A'BED téglalappal, ezek a szögek az A'BD szöggel is egyenlőek: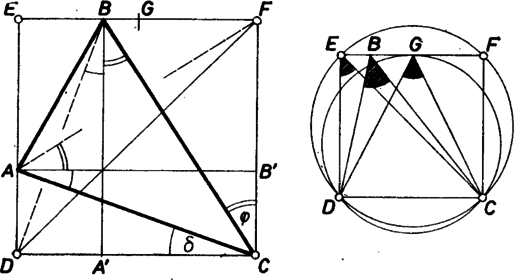

B'AC∢=ACD∢=A'BD∢.
Hasonlóan kapjuk, hogy
B'AF∢=BCF∢=A'BC∢.

 

 

Ezek szerint az ABC háromszög C-nél levő γ szöge és a BCD háromszög B-nél levő szöge 90∘-ra egészítik ki egymást. Ez utóbbi biztosan nagyobb 45∘-nál, hiszen B benne van a négyzet köré írható körben, így B-ből a CD oldal nagyobb szög alatt látszik, mint az E, F csúcsokból. A B-hez tartozó látószög akkor maximális, ha B azonos az EF oldal G felezőpontjával, ami a megengedett q=12(p+r) esetben fordul elő. Különben ugyanis B a CDG háromszög köré írható körön kívül helyezkedik el, hiszen ez a kör G-ben érinti az EF egyenest. Mivel cosCGD∢=0,6, CGD∢=53,13∘, így azt kaptuk, hogy
36,87∘≤γ<45∘.(1)

Az ABC háromszög B-nél levő β szöge nagyobb a CBD szögnél, hiszen tartalmazza azt. Emiatt β>45∘ és β+γ>90∘, vagyis az ABC háromszög A-nál levő α szöge kisebb 90∘-nál. Mivel α viszont nagyobb az ACF háromszög A-nál levő szögénél, α>45∘ és α+γ>90∘, vagyis β<90∘. Tehát
45∘<α,β<90∘.(2)

II. megoldás. Jelöljük az ACD, BCF szögeket δ-val, φ-vel, ezek tangensét λ-val, μ-vel:
λ=tgδ=q-pr-p,μ=tgφ=r-qr-p,
vagyis λ, μ pozitívak és λ+μ=1. A tangens függvényre vonatkozó addíciós képlet szerint
ctgγ=tg(90∘-γ)=tg(δ+φ)=λ+μ1-λμ,
tehát tgγ=1-λμ. Így tgγ mindenesetre kisebb, mint 1, és a λ+μ=1 feltétel miatt λ=μ=12 mellett minimális az értéke, amikoris tgγ=34, amiből γ-ra ismét az (1) alatti határokat kapjuk. Ugyancsak az addíciós képlet szerint
tgα=tg CAB'∢+tg B'AB∢1-tg CAB'∢tg B'AB∢=λ+μλ1-μ=1+μλ2,
és hasonlóan kapjuk, hogy tgβ=1+λμ2. Tehát tgα, tgβ nagyobb egynél, amiből α-ra és β-ra a (2) alatti határokat kapjuk. Ha λ tart 0-hoz, tgα, tgβ, tgγ értéke rendre ∞-be, 1-hez, 1-hez tart, tehát α értéke 90∘-hoz, β és γ pedig 45∘-hoz tart. Ha pedig μ tart 0-hoz, akkor β tart 90∘-hoz és α, γ tart 45∘-hoz. Eszerint az (1), (2) határok nem javíthatóak.